CK-12 Foundation
Limit of a Sequence: Finding the Limit of a Sequence (Part 3)
Limit the view of sequences on both sides of the axis. Learners explore an alternating sign sequence. Using a graphical display of the first 10 terms of the sequence, pupils determine the formula for the general term. they then use the...
CK-12 Foundation
Limit of a Sequence: Finding the Limit of a Sequence (Part 2)
What does it mean if young mathematicians cannot put the squeeze on a sequence? Learners investigate a divergent sequence and find the formula for the nth term. Using the definition of a limit of a sequence, pupils try to find the limit...
CK-12 Foundation
Limit of a Sequence: Finding the Limit of a Sequence (Part 1)
Put a squeeze on a sequence. An interactive provides a graphical display of a sequence. Using the graph, learners determine the algebraic expression for the sequence. Pupils use the general definition of a limit of a sequence to find the...
CK-12 Foundation
Finding the nth Term Given the Common Ratio and the First Term: Dominoes
Topple misunderstandings of geometric sequences. Using a context of creating ever-increasing sizes of dominoes, pupils develop a geometric sequence. The scenario provides the size of the first domino and the common ratio between...
CK-12 Foundation
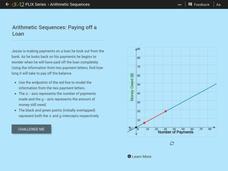
Arithmetic Sequences: Paying of a Loan
How long does it take to pay off a loan? Pupils use a graph to model the sequence associated with paying off a loan. Using the graph, learners determine the initial value and the common difference of the arithmetic sequence. The learners...
CK-12 Foundation
Sum Notation and Properties of Sigma: Cracking the Code
Help your class develop an understanding of sigma notation. Pupils match the sigma notation with the sums. Using the expanded sums, learners evaluate the summations. The scholars move on to prove a property of sums.
CK-12 Foundation
Solving Logarithmic Equations
Pupils follow a chain of reasoning in deconstructing a logarithmic equation step by step. Using their knowledge of logarithms, learners compare the solutions of logarithmic equations when the bases are changed.
CK-12 Foundation
Change of Base: River Logs
Using the answers to the challenge questions, class members work through simplifying a complex logarithmic expression that requires changing bases. Pupils drag values to fill in the steps to arrive at a numerical equivalent expression.
CK-12 Foundation
Existence: One-to-One Functions and Inverses
One-to-one means the answer is simple, right? Given four graphs, pupils use a vertical line to test each graph to find out if they are one-to-one. By using the resource, learners realize that not all one-to-one relations are functions....
CK-12 Foundation
Inverse Functions: Definition of Inverse Functions
Is the inverse of a function also a function? Pupils manipulate the graph of a function to view its inverse to answer this question. Using a horizontal and vertical line, class members determine whether the initial function is...
CK-12 Foundation
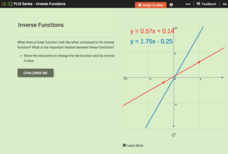
Inverse Functions
Provide a graphical view of inverses. Pupils manipulate points on a line and see the relationship of the graph with the graph of its inverse. Using the relationship between the graphs, scholars respond to questions concerning inverses...
CK-12 Foundation
Work and Force: Lifting a Bucket
How much work does it take to lift a bucket? An interactive presents a problem of lifting a bucket from the ground to the top of a building. Using their knowledge about work and integrals, pupils calculate the amount of work required to...
CK-12 Foundation
Volume by Disks: The Vase Case
Finding the volume is an integral characteristic of a vase. Using the idea that summing the areas of cross-sectional disks will calculate the volume of a rotational solid, pupils find the volume of a vase. Scholars determine the interval...
CK-12 Foundation
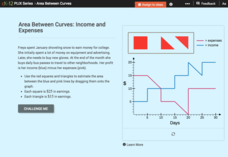
Area Between Curves: Income and Expenses
Use the area of polygons to calculate the area between curves. Pupils calculate areas under income and expense curves by filling the space with squares and right triangles. Using that information, they determine the profit related to the...
CK-12 Foundation
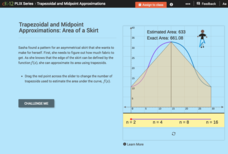
Trapezoidal and Midpoint Approximations: Area of a Skirt
When are trapezoids better than rectangles? Using trapezoids pupils approximate the area of fabric defined by a function. Just like with rectangles, learners realize the more trapezoids the more accurate the approximation. Scholars use...
CK-12 Foundation
Properties of Definite Integrals
Close your eyes and visualize a definite integral. An interactive provides a visualization of a function and definite integral on a closed interval. Pupils move one point of the interval in either the positive or negative direction....
CK-12 Foundation
Vector Projection: Hitting a Baseball
Hit a home run with a resource that is all fun and games. Learners apply an interactive to determine the horizontal component of the distance a baseball travels. They must consider vector projections for this task.
CK-12 Foundation
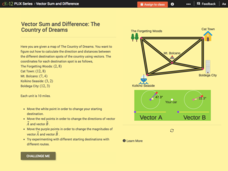
Vector Sum and Difference: The Country of Dreams
Find your way around using vectors. Scholars use an interactive to learn about vector addition. They answer a set of questions about modeling a route on a map using vectors.
CK-12 Foundation
Explicit Formulas: Tiles for Writing nth Term in a Sequence
Build an explicit formula using tiles. Pupils develop a tile representation of a term within a sequence given figures of previous terms. Using the diagrams, learners develop the explicit formula by recognizing the common difference and...
CK-12 Foundation
Logarithmic Differentiation: Graphing the Derivative of a Logarithm
Log the values of the derivative of a logarithm. The interactive plots the derivative of the natural logarithm. Learners first determine the derivative of natural logarithm and the general logarithm. Using the formulas for the...
CK-12 Foundation
Logarithm Properties: The Log Properties
Roll a log into an equivalent expression. Given four expanded logarithmic expressions, pupils write an equivalent condensed expression. They identify which properties allows for the simplification.
CK-12 Foundation
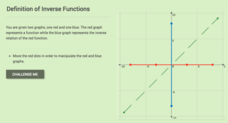
Definition of Inverse Functions
Investigate the definition of inverse functions graphically. Using the interactive, scholars create a graph of a function and view its resulting inverse. They then determine whether a group of functions have inverses that are also...
CK-12 Foundation
Differential Equations Representing Growth and Decay: Rice Legend
The legend of a wise man who asks a king for rice as a reward presents a context to study exponential solutions to differential equations. Pupils move quantities of rice to a chessboard and calculate the amount of rice for each day. To...
CK-12 Foundation
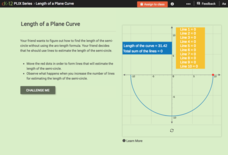
Length of a Plane Curve
Challenge your class to use straight lines when estimating the length of a curve. An engaging interactive allows individuals to place line segments one after another along the arc. Learners determine that the more lines used, the better...