CK-12 Foundation
Volume by Cross Section: Volume of the Cone
Discover another way to find the volume of a cone. Pupils explore how the area of a cross section changes as it moves through a cone. The interactive uses that knowledge to develop the integral to use to find the volume of the cone....
CK-12 Foundation
Method of Cylindrical Shells
Approximate the volume of a solid of revolution. Using a method similar to approximating the area under a curve, pupils investigate the volume of a solid of revolution. The learners use a given definite integral to find the volume of...
CK-12 Foundation
Area Sums: Estimation with Rectangles
The more rectangles, the better the estimate. Using the interactive, pupils explore estimating the area under a curve using left-hand sums. Learners respond to challenge questions on how to get better estimates using the same technique.
CK-12 Foundation
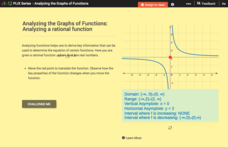
Analyzing the Graphs of Functions: Analyzing a Rational Function
Shift the function and transform the key features of the graph. By translating the graph of the rational function, class members find out how the key features alter. Pupils determine the domain, range, asymptotes, and intervals of...
CK-12 Foundation
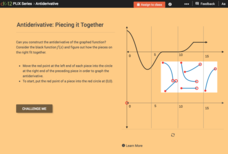
Antiderivative: Piecing it Together
Build a function backwards. Given a graph of the derivative of a function, pupils piece together a graph of the original function, the antiderivative. Learners use their graphs and the graphs of the derivatives to answer questions about...
CK-12 Foundation
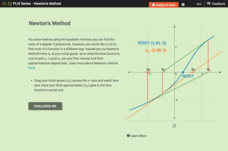
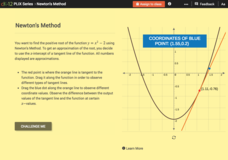
Newton's Method
Does the accuracy of the first guess make a difference down the line? Learners investigate the effects of the iterative process of finding roots, using Newton's Method. By moving the initial guess of a root on a graph, pupils observe the...
CK-12 Foundation
Absolute Extrema and Optimization: Building the Biggest Box
Optimally, you want the largest box. Given a square piece of box material, pupils determine the size of congruent squares to cut out of the corners to create a box with the greatest volume. Learners determine the equation of the volume...
CK-12 Foundation
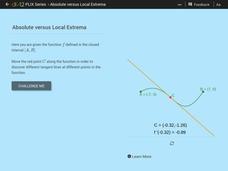
Absolute Versus Local Extrema
Get the class to take an extreme look at functions. The interactive presents a function on a closed interval with a movable tangent line. Using the given function, pupils determine the extrema, critical points, and points of inflection.
CK-12 Foundation
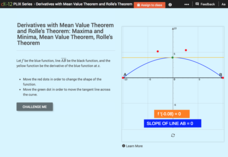
Derivatives with Mean Value Theorem and Rolle's Theorem: Maxima and Minima
Rolle with the mean values and derivatives. Scholars complete the statements of Rolle's Theorem and the Mean Value Theorem. Using the interactive to illustrate scenarios, pupils respond to questions concerning the theorems in terms of...
CK-12 Foundation
Related Rates of Car Speeds
Speed up your pupils' understanding of derivatives. Two cars travel in perpendicular distances to each other. With the aid of the interactive, learners visualize the situation. Pupils use the derivative to calculate the instantaneous...
CK-12 Foundation
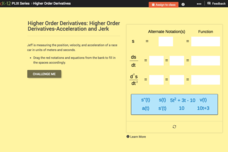
Higher Order Derivatives—Acceleration and Jerk
Accelerate your class through finding the second derivative. Using a bank of equations, pupils determine the equations for distance, velocity, and acceleration and their associated function notations. With the equations, learners answer...
CK-12 Foundation
Chain Rule
Keep it on the chains. Pupils work through the steps in the chain rule using the interactive as a guide. Learners identify the two composed functions and their associated derivatives from a set of choices. They continue on to build the...
CK-12 Foundation
Constant, Identity, and Power Rules: Power Rule
Learn to gain power in finding derivatives. The resource introduces the power rule. Using the sliders in the interactive, pupils create polynomial functions and find their derivatives. Given the derivative of a polynomial, learners...
CK-12 Foundation
Derivatives of Trigonometric Functions: Derivative of sin(x)
Graphically find the derivative of sin(x). Using the interactive, pupils graph the slope of the tangent line to the sine function. Class members use the resulting graph to determine the derivative of the sine function. They verify their...
CK-12 Foundation
Tangent Line Approximation: Estimating Square Roots
Estimating a square root is as easy as evaluating a linear equation. Using the derivative of the square root function, pupils calculate an estimation of square roots. Class members determine the equation of the tangent line at the value...
CK-12 Foundation
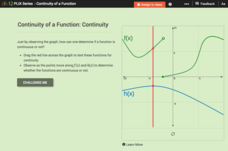
Continuity of a Function: Continuity
Does the point continually move along the graph? Pupils drag a line across two functions to determine whether they are continuous or not. They answer questions about the properties of continuous and discontinuous functions. Using their...
CK-12 Foundation
Linear, Quadratic, and Cubic Models: The Box Model
Models make math manageable. Individuals investigate a cubic function that models the volume of a cube through the interactive.
CK-12 Foundation
Newton's Method
Use an iterative process to find an approximation of a square root. Pupils use the interactive to find an approximation to find the positive root of a quadratic function with Newton's method. With the graphs, learners position the...
CK-12 Foundation
Infinite Limit Type: Asymptotes and End Behavior Question
There are an infinite number of reasons to use the resource. Scholars drag vertical and horizontal lines to the graph of a rational function to identify all asymptotes. They investigate the connection between asymptotes and limits to...
CK-12 Foundation
Infinite Limit Type: Properties of Limits
Limits can provide some valuable information about graphs. A slider interactive lets learners see the behavior of a graph around asymptotes. They investigate relationships between limits and asymptotes.
CK-12 Foundation
One-Sided Limit Type: One-Sided Limits
Not everything that's one-sided is bad. A slider interactive aids learners in investigating one-sided limits from graphs. A set of challenge questions assesses their understanding of the relationship between one- and two-sided limits.
CK-12 Foundation
Evaluate Limits Using Graphs and Tables: Where Is That Limit?
Limits are made easy through graphs and tables. An easy-to-use interactive lets users change a function on a coordinate plane. They relate graphs and tables to the limit at a specific value.
CK-12 Foundation
Concept of Limit: Limit Notation
Limits to infinity are simple to find if you can compare numerators and denominators. Users of the interactive drag expressions to match with their limit as x approaches infinity. A set of challenge questions assesses their groupings.
CK-12 Foundation
Find Imaginary Solutions: Imaginary Zeros
The resource is the real deal. Individuals investigate the imaginary zeros of f(x) = x^2 + 1. They accomplish this task by using an interactive that shows input values x = a + bi and output values x^2 + 1 on a complex plane.