CCSS Math Activities
Smarter Balanced Sample Items: High School Math – Target M
Your knowledge of graphs is a function of how much you try. Young mathematicians work on a set of 12 questions that covers graphing functions, comparing functions, and rewriting functions in different forms to determine key features....
CK-12 Foundation
Infinite Limit Type: Asymptotes and End Behavior Question
There are an infinite number of reasons to use the resource. Scholars drag vertical and horizontal lines to the graph of a rational function to identify all asymptotes. They investigate the connection between asymptotes and limits to...
CK-12 Foundation
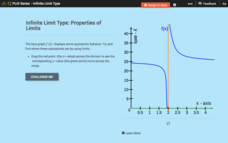
Infinite Limit Type: Properties of Limits
Limits can provide some valuable information about graphs. A slider interactive lets learners see the behavior of a graph around asymptotes. They investigate relationships between limits and asymptotes.
Desmos
Desmos Graphing Calculator
They say a graph is worth a thousand points. The interactive allows users to graph a wide variety of functions and equations. Using the included keyboard or typing directly into the list, learners determine the graph of a function....
GeoGebra
Getting on the Right Wavelength
Predict an equation that waves up and down. Pupils set the height, radius, and period of a Ferris wheel. The learners write a sine equation to match the graph of the height of a point on the wheel as a function of time. Running the...
CK-12 Foundation
Infinite Limit Type: Evaluating Limits of Rational Functions
Rational functions become less mysterious when you know about limits. Individuals use an interactive to move a rational function on a coordinate plane and to investigate function values for certain x-values. They see how the limit...
GeoGebra
More Ferris Wheels
Take a ride on a Ferris wheel. Using sliders to adjust the parameters of a Ferris wheel, pupils investigate the height of a point over time. The interactive traces out the curve on a time-height graph. Learners use what they learned to...
CK-12 Foundation
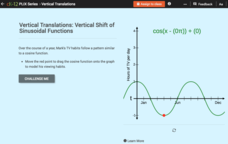
Vertical Translations: Vertical Shift of Sinusoidal Functions
Create a shift in TV viewing habits. The interactive presents a cosine model of an individual's TV viewing habits during a year. Class members move the model to reflect given conditions. Finally, they determine key features from the...
CK-12 Foundation
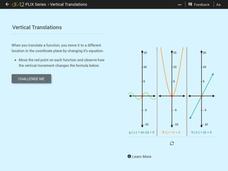
Vertical Translations
Change the y-intercept by adding a constant to the function. Individuals move three functions vertically along the y-axis. As they observe how the equation of the functions change with the vertical movement, learners determine how to...
CK-12 Foundation
Horizontal Translations or Phase Shifts: Cosine
If cosine is shifted, how is its equation affected? Learners manipulate the graph of cosine by moving the y-intercept to different locations on the coordinate plane. Pupils determine the new equation that models the shifts.
CK-12 Foundation
Horizontal Translations or Phase Shifts: Horizontal Translations
Find out what causes a function to slide. Pupils move a function along the x-axis and see the resulting change in its equation. Scholars determine the effects that the translation has on the intercepts, domain, and range of the function.
CK-12 Foundation
Horizontal Translations or Phase Shifts: Sine
Shift a trigonometric function and find its new equation. Pupils translate a sine function on a graph. The scholars determine the equation of the function that represents the translated graph and observe the connection between a...
CK-12 Foundation
Vertical Translations: Translating a Square Root Function
How does the equation of a function reflect translations? Scholars manipulate the starting point of the parent square root function before determining the new equations that result from the translations. Class members also determine the...
CK-12 Foundation
Horizontal Translations or Phase Shifts: Horizontal and Vertical Translations
It is all about the shift. Pupils translate the graph of a cubic function to different marked locations on the plane and determine the new equation that represents the shifts. The activity is designed to encourage individuals begin to...
CK-12 Foundation
Horizontal Translations or Phase Shifts: Tangent
Patterns can be shifty! Find the pattern when shifting the graph of tangent. Pupils move the graph of tangent to different locations on the coordinate plane. They observe what happens to the function and its vertical asymptotes before...
CK-12 Foundation
Changes in Period and Amplitude of the Sine Function
How does a change in amplitude or period affect the equation of a sine function? Scholars move sliders to change the frequency and period of the sine function. The interactive displays the resulting equation, and pupils determine the...
CK-12 Foundation
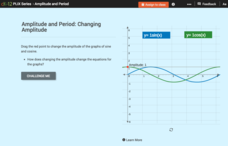
Sine Graph and Cosine Graph: Changing Amplitude
Scholars manipulate the amplitude of the graphs of sine and cosine, notice how the change in amplitude is reflected in their graphs, and answer several questions about the concept they noticed.
Mathematics Vision Project
Features of Functions
What are some basic features of functions? By looking at functions in graphs, tables, and equations, pupils compare them and find similarities and differences in general features. They use attributes such as intervals of...
Mathematics Vision Project
Linear and Exponential Functions
Provide a continuous progression to linear and exponential functions. Pupils continue to work with the discrete functions known as sequences to the broader linear and exponential functions. The second unit in a series of nine provides...
CK-12 Foundation
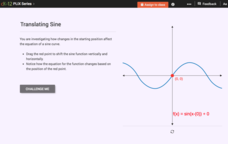
Translating Sine and Cosine Functions: Translating Sine
Learn how to slide sine back and forth and up and down. Pupils move the starting point of a graph of sine vertically and horizontally. They investigate the changes to the equation of the graph in relationship to the translation. They...
CK-12 Foundation
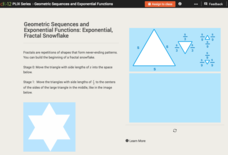
Exponential Growth: Exponential, Fractal Snowflakes
Examine an exponential growth model. Using a fractal, learners calculate the perimeters of each stage. When comparing the consecutive perimeters, a pattern emerges. They use the pattern to build an equation and make conclusions.
CK-12 Foundation
Exponential Decay: Cool Sunglasses
Who wouldn't want to wear four pairs of sunglasses? Each pair of sunglasses reduces the percent of incoming light by one-half. An interactive tutorial helps young mathematicians build a graph that models this scenario. They then explore...
CK-12 Foundation
Logarithms: Logarithm Triangle
Study logarithmic properties using a triangle. A clever manipulative shows how a triangle can represent the three parts of a logarithmic or exponential equation. Pupils review the concept and then answer guiding questions to further...
Teach Engineering
Biomimicry and Sustainable Design - Nature is an Engineering Marvel
Discover how copying nature can be beneficial to humans. Scholars read articles about examples of biomimicry and its potential applications. Along the way, they learn about Nature's Nine Laws and how they relate to biomimicry. This is...