CK-12 Foundation
Pythagorean Theorem to Determine Distance: Tree Shadows
Why is that shadow getting longer? Determine the changes in the length of a shadow as the sun changes position in the sky. Individuals use an interactive to calculate the length of a shadow at different times during the day via the...
CK-12 Foundation
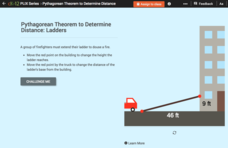
Pythagorean Theorem to Determine Distance: Ladders
Young mathematicians to the rescue! Pupils use an interactive to find lengths relating a ladder against a building. The problems involve determining how long a ladder must be to reach a given floor to what floor can a given ladder reach.
Bowels Physics
Methods of Motion
How could you earn a $6,000,000 speeding ticket? This presentation uses an analogy that relates speed in the universe to the cost of a speeding ticket. Scholars ultimately understand that motion is relative. Also covered is the concept...
EngageNY
End-of-Module Assessment Task: Grade 6 Math Module 3
The last installment of a 21-part module is an end-of-module assessment. Individuals show their understanding of positive and negative numbers on the number line, absolute value, and the coordinate plane in a variety of contexts.
EngageNY
Problem Solving and the Coordinate Plane
Class members investigate rectangles on the coordinate plane. They determine the length of line segments in the coordinate plane with the same x-coordinate or same y-coordinate and then solve geometric problems involving perimeter and...
EngageNY
Distance on the Coordinate Plane
Scholars learn how to find the distance of vertical and horizontal line segments on the coordinate plane in the 19th installment of a 21-part module. The use of absolute value comes in handy.
EngageNY
Absolute Value—Magnitude and Distance
Do you want to use the resource? Absolutely. Scholars learn about absolute value and its relation to magnitude and distance on a number line. They compare numbers in context by applying absolute value.
McGraw Hill
Stellar Parallax Interactive
How are scientists able to measure distances between stellar bodies? Turns out it's not very easy! Learners explore the process of trigonometric parallax as the method of determining these distances. They experience the same challenges...
McGraw Hill
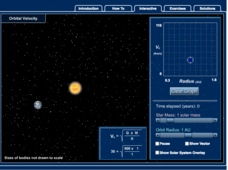
Orbital Velocity Interactive
Why does it take Pluto 90,000 days to orbit the sun, but it only takes Mercury 88 days? An interactive lesson helps pupils find a connection between the speed of orbit and distance a planet is from the sun. The simulation allows for...
Laboratory for Atmospheric and Space Physics
Orbit Simulator
Researchers think they have evidence of a new planet deep in our solar system that is the size of Neptune and orbits the sun far beyond Pluto. The orbit simulator shows the orbits of our well-known planets, as well as Pluto and the comet...
EngageNY
Getting the Job Done—Speed, Work, and Measurement Units II
How fast is your class? Learners determine the amount of time it takes individuals to walk a given distance and calculate their speeds. Pupils solve distance, rate, and time problems using the formula and pay attention to the rate units.
Noyce Foundation
Movin 'n Groovin
Examine the consequences of varying speed. An engaging set of five problem sets challenges young mathematicians by targeting a different grade level from K-12. In the initial lesson, scholars make conclusions about the time it takes two...
Noyce Foundation
First Rate
Explore distance and time factors to build an understanding of rates. A comprehensive set of problems target learners of all grade levels. The initial problem provides distance and time values and asks for the winner of a race. Another...
Virginia Department of Education
Distance and Midpoint Formulas
Small groups work through two guided activities to derive the distance and midpoint formulas for the coordinate plane. The activities begin with concrete examples and move to abstract.
EngageNY
Distance on the Coordinate Plane
Apply the Pythagorean Theorem to coordinate geometry. Learners find the distance between two points on a coordinate plane by using the Pythagorean Theorem. The vertical and horizontal change creates a right triangle, which allows...
EngageNY
End-of-Module Assessment Task: Grade 8 Mathematics (Module 7)
It's time to discover what your classes have learned! The final lesson in the 25-part module is an assessment that covers the Pythagorean Theorem. Application of the theorem includes distance between points, the volume of...
University of Colorado
Can Photosynthesis Occur at Saturn?
In the 19th activity of 22, learners determine if distance from a light source affects photosynthesis. Participants capture oxygen in straws and find that the amount of water the gas displaces is proportional to the rate of photosynthesis.
EngageNY
A Critical Look at Proportional Relationships
Use proportions to determine the travel distance in a given amount of time. The 10th installment in a series of 33 uses tables and descriptions to determine a person's constant speed. Using the constant speed, pupils write a linear...
Balanced Assessment
All Aboard
Pupils must graph the location of a train using the time given a timetable. They analyze the different legs of the trip, graph the return trip, and compare the two graphs. The lesson ends with a discussion of similarities and differences...
Balanced Assessment
Dinner Date
Determine just how far to run before dinner. The short assessment asks pupils to determine the distance a person can jog in the time left before dinner. To answer the question, scholars determine the distance if the person jogs one way...
Balanced Assessment
Ford and Ferrari
Which is faster, a Ford or a Ferrari? The short assessment has pupils analyze graphs to determine the rates of change between the two. Individuals interpret the rates of change within the context of speeds of the cars and develop a map...
EngageNY
Modeling with Inverse Trigonometric Functions 1
Where should I stand to get the best view? Pupils use inverse trigonometric functions to determine the horizontal distance from an object to get the best view. They round out the lesson by interpreting their answers within context.
University of Colorado
Planetary Distances on the Playground
Earth is 149,600,000 km, or 92,957,130.4 miles, from the sun. Young astronauts create an interactive model to learn the distances between planets. Nine groups, each representing a different planet, are spread around at class-calculated...
EngageNY
Modeling Using Similarity
How do you find the lengths of items that cannot be directly measured? The 13th installment in a series of 16 has pupils use the similarity content learned in an earlier resource to solve real-world problems. Class members determine...