Flipped Math
Calculus AB/BC - Derivatives of tan(x), cot(x), sec(x), and csc(x)
Continue to differentiate the rest of the trigonometric functions. Pupils see the derivatives of the other four trigonometric functions and begin to memorize the rules. Learners see examples that show that the calculus portion of a...
Lane Community College
Review Sheets: Trigonometry
Review guide, practice test, homework packet? Yes, yes, and yes as it's all possible with a wonderful trigonometry packet. Every type of problem is there, starting from the unit circle and ending with conic sections.
Flipped Math
Unit 7 Review: Right Triangles
It is all right to spend some time with a review. After watching a short review video covering the materials from the unit, pupils work through 23 review problems. Scholars work on problems involving the Pythagorean Theorem and its...
Flipped Math
Unit 10 Review: Graphing Sine and Cosine
Go up and down with a review. Learners review finding the amplitude, midline, period, and frequency of sinusoidal functions and use that information to draw graphs. Pupils arrive at equations for function from graphs. They finish up the...
Flipped Math
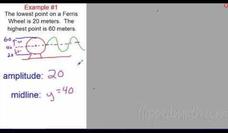
Modeling with Trig Functions
Find out what to do with Ferris wheels that keep going up and down. Individuals learn how to determine the frequency of a trigonometric function. Pupils use their knowledge of trigonometric functions to model periodic motions like Ferris...
Flipped Math
Reference Triangles
It is all about where the side is located. Pupils use their knowledge of angles in standard position to find reference angles. They use the Pythagorean Theorem to find lengths along a terminal side of an angle to determine the exact...
Flipped Math
Intro to Trigonometry
Expand trigonometric ratios beyond right triangles. Pupils start with a review of trigonometric ratios and then take a look at angles in standard position to determine their measurements. Scholars discover how to find coterminal angles...
Radford University
REALLY Tall!
Conduct indirect measurements three ways. Working in groups, pupils come up with different ways to measure three tall objects indirectly. The teacher provides measurement information requested by the teams, and learners then calculate...
Radford University
Georgia Peaches and California Dreamin’
Plant the fruits of trigonometry. Pairs work through the process of finding the best place to plant fruit trees on a piece of property. The scholars must take into consideration the location of the property and the solar zenith angle. To...
Radford University
How Tall Is It?
Find the height from afar. Teams role play as summer interns to find the height of a set of windows from the outside. Scholars must first determine how to find the height with the available tools. After determining a strategy involving...
Rice University
Precalculus
Take a step beyond Algebra 2. Learners use the eBook to learn concepts from the typical Precalculus course. Content starts off with a short review of functions in general and moves on to the basic functions, finishing up with more...
Concord Consortium
Sine Solution
How many times can eager mathematicians catch the waves? Pupils find the solutions of three different trigonometric equations. They then determine the effect of the slope of a line that intersects a trigonometric function and the number...
Concord Consortium
Line of Sight
There's no way around it—learners must use trigonometry to model the line of sight around a race track! Using the starting line as the origin, pupils model the straight line distance to any car using a trigonometric expression. The...
Project Maths
The Unit Circle
It's not just any circle—it's the unit circle. The fourth lesson in the series is an introduction to the famous unit circle. While working through a series of activities, young scholars learn the components of the unit circle and how to...
Alabama Learning Exchange
"I Saw the Sine"
Discover trigonometric ratios that complement each other. Using two videos, the activity introduces the trigonometric ratios. The class discovers the relationship between the sine and cosine of complementary angles.
CK-12 Foundation
Derivatives of Trigonometric Functions: Derivative of sin(x)
Graphically find the derivative of sin(x). Using the interactive, pupils graph the slope of the tangent line to the sine function. Class members use the resulting graph to determine the derivative of the sine function. They verify their...
CK-12 Foundation
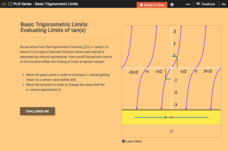
Basic Trigonometric Limits: Evaluating Limits of tan(x)
Chase a periodic moving limit. Learners graphically determine the limit of the tangent function at different input values. Using sliders, pupils find out whether the tangent function approaches the same value from the left and the right....
GeoGebra
More Ferris Wheels
Take a ride on a Ferris wheel. Using sliders to adjust the parameters of a Ferris wheel, pupils investigate the height of a point over time. The interactive traces out the curve on a time-height graph. Learners use what they learned to...
CK-12 Foundation
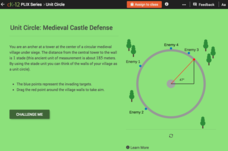
Unit Circle: Medieval Castle Defense
Who needs a plan — let trigonometry protect you! Pupils determine the angle of an approaching enemy to a village wall. The scholars determine the exact value of trigonometric functions for the angle. Class members use trigonometry to...
CK-12 Foundation
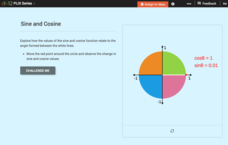
Domain, Range, and Signs of Trigonometric Functions: Sine and Cosine
Is there a relationship between the sign of sine and cosine and the angle on the unit circle? Scholars use an interactive to see the value of sine and cosine within different quadrants. they then use the information to determine the...
CK-12 Foundation
Reciprocal Identities
Get a better understanding of the trigonometric functions by taking a look at the flip side. Pupils create angles within a unit circle and compare the values of the standard trigonometric functions to their reciprocal functions. The...
CK-12 Foundation
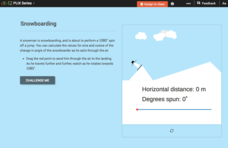
Trigonometric Functions of Angles Greater than 360 Degrees: Snowboarding
Spin through the trigonometric functions. Scholars determine the angle of rotation a snowboarding snowman makes at various distances in his jump. The class members then calculate the values of trigonometric functions for those angles.
CK-12 Foundation
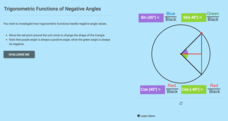
Trigonometric Functions of Negative Angles
When is the trigonometric value of a negative angle the same as the positive angle? Pupils compare the values of trigonometric functions for different angles and their negatives. The interactive resource provides a visual display to make...
CK-12 Foundation
Horizontal Translations or Phase Shifts: Cosine
If cosine is shifted, how is its equation affected? Learners manipulate the graph of cosine by moving the y-intercept to different locations on the coordinate plane. Pupils determine the new equation that models the shifts.