CK-12 Foundation
Horizontal Translations or Phase Shifts: Sine
Shift a trigonometric function and find its new equation. Pupils translate a sine function on a graph. The scholars determine the equation of the function that represents the translated graph and observe the connection between a...
CK-12 Foundation
Horizontal Translations or Phase Shifts: Tangent
Patterns can be shifty! Find the pattern when shifting the graph of tangent. Pupils move the graph of tangent to different locations on the coordinate plane. They observe what happens to the function and its vertical asymptotes...
CK-12 Foundation
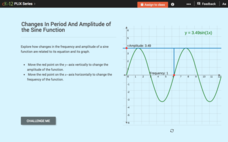
Changes in Period and Amplitude of the Sine Function
How does a change in amplitude or period affect the equation of a sine function? Scholars move sliders to change the frequency and period of the sine function. The interactive displays the resulting equation, and pupils determine the...
CK-12 Foundation
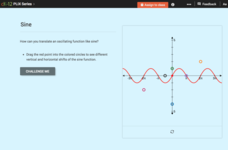
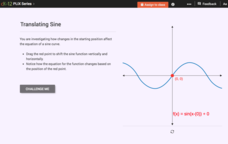
Translating Sine and Cosine Functions: Translating Sine
Learn how to slide sine back and forth and up and down. Pupils move the starting point of a graph of sine vertically and horizontally. They investigate the changes to the equation of the graph in relationship to the translation. They...
CK-12 Foundation
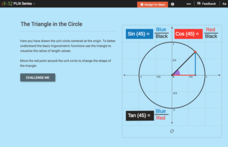
Trigonometric Functions and Angles of Rotation: The Triangle in the Circle
Go around the unit circle and create triangles. Pupils move a point around the unit circles to visualize the triangle associated with the angle in standard position. The three main trigonometric functions are defined in terms of the legs...
CK-12 Foundation
Right Triangles, Bearings, and Other Applications: Sailing Race
Help your class get their bearings when it comes to right triangles. Pupils determine distances traveled or components given the bearing of a sailboat using an interactive. The scholars develop a sense of finding the bearings of a given...
CK-12 Foundation
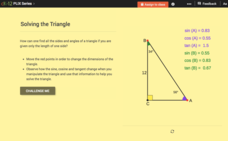
Pythagorean Theorem for Solving Right Triangles: Solving the Triangle
Observe the change in the trigonometric ratios as angles vary. An interactive provides the values of trigonometric ratios for both acute angles in a right triangle. Pupils create a right triangle to match given criteria and find the...
CK-12 Foundation
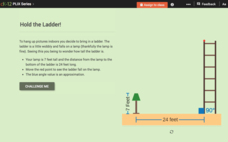
Secant, Cosecant, and Cotangent Functions: Hold the Ladder!
Determine the length of a falling ladder. Pupils use an interactive to find the angle a ladder makes with the floor after it falls to answer questions. The scholars use the triangle formed in the interactive to determine values of...
CK-12 Foundation
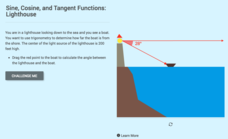
Sine, Cosine, and Tangent Functions: Lighthouse
How far is that boat from the lighthouse? Scholars create diagrams to represent a scenario given the angle of depreciation from a lighthouse to a boat. Learners apply the basic trigonometric functions to find various distances...
CK-12 Foundation
Angles of Elevation and Depression: Fly-By Calibration
Determine the distance between two trees from afar. Pupils use an interactive resource to create two right triangles using trees and a plane. They determine the horizontal legs of each triangle to find the distance between the two trees.
CK-12 Foundation
Basic Trigonometric Functions: Ladder Length
Climb the ladder to trigonometry. The interactive introduces trigonometric ratios and finding lengths of sides of right triangles created by a ladder and a building. Learners use the interactive to create triangles by moving the top of...
McGraw Hill
Stellar Parallax Interactive
How are scientists able to measure distances between stellar bodies? Turns out it's not very easy! Learners explore the process of trigonometric parallax as the method of determining these distances. They experience the same challenges...
Illustrative Mathematics
Hours of Daylight 1
The midline of the mathematical model of the number of hours of sunlight is not 12 hours. Pupils use the modeling cycle to determine a function that will model the number of hours of sunlight at a location of their choosing. Using...
Illustrative Mathematics
As the Wheel Turns
Determine the location of a point on a moving wheel. The task challenges groups to determine the horizontal and vertical locations of a point on the edge of wheel that is moving. Teams first determine a function that will model the...
Illustrative Mathematics
Sum and Difference Angle Formulas
Need practice deriving trigonometric angle formulas? With this worksheet, pupils derive the sum and difference formulas for cosine and tangent and the difference formula for sine. Scholars use the sine sum formula and other known...
EngageNY
Waves, Sinusoids, and Identities
What is the net effect when two waves interfere with each other? The lesson plan answers this question by helping the class visualize waves through graphing. Pupils graph individual waves and determine the effect of the interference...
EngageNY
End-of-Module Assessment Task: Pre-Calculus Module 4
Challenge your scholars to show what they know about the Law of Sines, Law of Cosines, and inverses. The six-question assessment is the last in a series of 16. Pupils find the area of triangles and show that the Law of Sines and Law of...
EngageNY
Modeling with Inverse Trigonometric Functions 1
Where should I stand to get the best view? Pupils use inverse trigonometric functions to determine the horizontal distance from an object to get the best view. They round out the lesson by interpreting their answers within context.
EngageNY
Inverse Trigonometric Functions
Build on the understanding of finding angles using trigonometric ratios. Pupils develop the definitions of inverse trigonometric functions by restricting their domains in the 13th lesson of a 16-part series. They use inverse functional...
EngageNY
Putting the Law of Cosines and the Law of Sines to Use
Use the Law of Cosines and the Law of Sines to solve problems using the sums of vectors. Pupils work on several different types of real-world problems that can be modeled using triangles with three known measurements. In the process,...
EngageNY
Law of Cosines
Build upon the Pythagorean Theorem with the Law of Cosines. The 10th part of a 16-part series introduces the Law of Cosines. Class members use the the geometric representation of the Pythagorean Theorem to develop a proof of the Law of...
EngageNY
An Area Formula for Triangles
Use a triangle area formula that works when the height is unknown. The eighth installment in a 16-part series on trigonometry revisits the trigonometric triangle area formula that previously was shown to work with the acute triangles....
EngageNY
Addition and Subtraction Formulas 1
Show budding mathematicans how to find the sine of pi over 12. The third lesson in a series of 16 introduces the addition and subtraction formulas for trigonometric functions. Class members derive the formulas using the distance...
EngageNY
Properties of Trigonometric Functions
Given a value of one trigonometric function, it is easy to determine others. Learners use the periodicity of trigonometric functions to develop properties. After studying the graphs of sine, cosine, and tangent, the lesson connects...