Curated OER
Ball Toss Activity
Pupils collect data from tossing a ball into the air. Using a data collection device, they graph the data, set a window, and analyze the height of the toss, how long the ball was in the air, etc. They then find an equation that models...
Curated OER
Let's Play Some Ball!
Pupils review horizontal and vertical shifts of a parabola and how they effect a specific quadratic formula. They play a basketball review game in which they try to find the right quadratic equation for a given problem in order to earn...
Curated OER
Storefront Signs
Learners practice finding the areas and patterns within a square and explore the concept of quadratic functions. They observe and record the area values in a table, plot a graph of Area versus Distance and complete a variety of student...
Curated OER
Quadratic Functions - Max and Min
Pupils identify the maxima and minima of quadratic functions. After a teacher explanation and demonstration of quadratic functions, students solve quadratic equations and graph the solution to find the maxima and minima of each...
Curated OER
Functions and Applications: Maximum Quadratic functions
In this maximum of quadratic equations worksheet students compute the maximum height of 5 independent events. Each problem uses a golf game as the setting. Students use a quadratic equation to solve the problems.
Curated OER
Discriminant and Quadratics
In this quadratic equation, students find the discriminant using the formula given and identify how many solutions a quadratic function will have. There are 3 problems with answers and examples.
Curated OER
Mirror Curvature
Students investigate parabolas as the shape of a telescopic mirror. In this Algebra I/Algebra II lesson, students explore the relationship between the coefficients of a quadratic function and the shape and position of the parabolic...
Curated OER
SkyHighScrapers
Students investigate quadratic functions. In this Algebra I/Algebra II lesson, students determine the equation of a quadratic function that closely matches a set of points. Students investigate the necessary information that...
Curated OER
Telescope #2
Students investigate parabolas as the shape of a telescopic lens. In this Algebra I/Algebra II lesson, students explore the relationship between the coefficients of a quadratic function and the shape and position of the parabolic...
Curated OER
"Ball Bounce" Quadratic Functions
Young scholars manipulate a ball and explore quadratic functions. In this algebra lesson, students analyze the graph of a quadratic function. They identify quadratic properties.
Curated OER
Worksheet 6, Graphing Functions
For this algebra worksheet students graph a given function by completing the square. They analyze a function and tell the axis of symmetry, the intercepts, and vertex. Students identify the maximum or minimum of a graph. Students...
Curated OER
Reflections of a Quadratic Function
Young scholars are asked to explain the relationship between f(s) and f (-x). They are asked to determine how the equation of f(x) differs from the equation of f(-x). Students determine the conditions when f(x) is the same as f(-x). They...
Richland Community College
Richland Community College: Algebra Lecture Notes
This site from Richland Community College provides lecture notes to a class on Algebra. It covers a wide array of topics including functions, quadratic equations, inequalities, and much more.
William Mueller
William Mueller: Families of Functions
Meet the Function Family! Each member of the family has examples of their graphs and descriptions of the types of real-world situation that produce those graphs.
![Pbs Teachers: Toothpicks and Transformations [Pdf] Lesson Plan](https://d15y2dacu3jp90.cloudfront.net/images/attachment_defaults/resource/large/FPO-knovation.png "Pbs Teachers: Toothpicks and Transformations [Pdf] Lesson Plan")
PBS
Pbs Teachers: Toothpicks and Transformations [Pdf]
Using calculators, students investigate quadratic functions using geometric toothpick designs in this lesson that with a review of transformations of quadratic functions, vertical and horizontal shifts, and stretches and shrinks.
Student Achievement Partners
Student Achievement Partners: Penny Circle Task [Pdf]
Students will explpre models and understand the difference between quadratic, exponential, and linear models in this lesson.
Other
Desmos: Quadratic Bundle
A collection of activities where students investigate quadratic relationships. Activities explore uses of quadratic relationships, features of parabolas and how to describe them, graphing quadratic functions, a marble activity with...
Varsity Tutors
Varsity Tutors: Hotmath: Practice Problems: The Discriminant
Thirty-eight problems present a variety of practice working with discriminant. They are given with each step to the solution cleverly revealed one at a time. You can work each step of the problem then click the "View Solution" button to...
Math Medics
S.o.s. Math: Quadratic Equations
Defines root of a quadratic equation. Portrays graphically what quadratic roots look like. Tutorial includes two basic examples where roots are discovered, and links to pertinent topics elsewhere on the site and a math forum organized by...
Varsity Tutors
Varsity Tutors: Hotmath: Practice Problems: Quadratic Functions
Twenty problems present a variety of problems working with various aspects of quadratic functions. They are given with each step to the solution cleverly revealed one at a time. You can work each step of the problem then click the "View...
Texas Education Agency
Texas Gateway: Determining Parent Functions (Verbal/graph)
Given a graph or verbal description of a function, the student will determine whether the parent function is quadratic or linear.
Texas Education Agency
Texas Gateway: Domain and Range for Quadratic Functions: Restricted Domain/range
Given a situation that can be modeled by a quadratic function or the graph of a quadratic function, the student will determine restrictions as necessary on the domain and range of the function.
Texas Education Agency
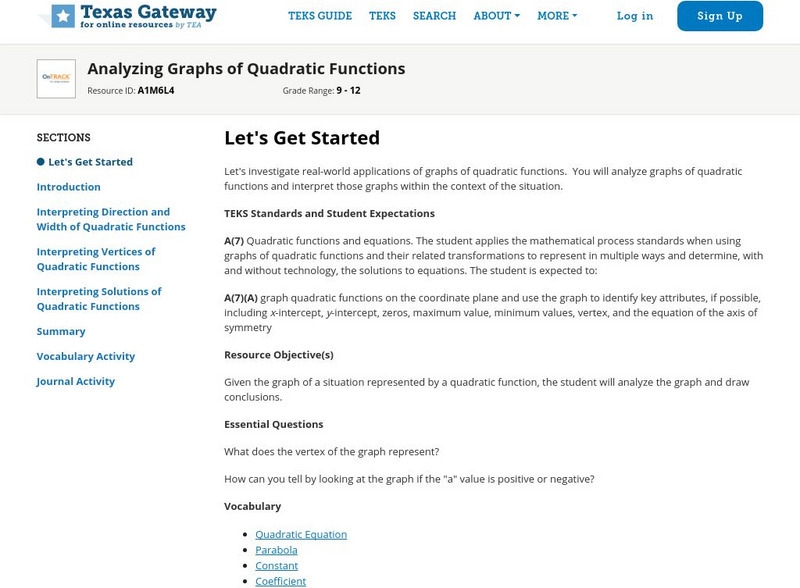
Texas Gateway: Analyzing Graphs of Quadratic Functions
Given the graph of a situation represented by a quadratic function, the student will analyze the graph and draw conclusions.
Texas Education Agency
Texas Gateway: Analyzing the Effects of Changes in "A" on the Graph Y=ax^2 + C
Given verbal, graphical, or symbolic descriptions of the graph of y = ax^2 + c, the student will investigate, describe, and predict the effects on the graph when "a" is changed.