Concord Consortium
Always, Sometimes, Never
Do your learners always, sometimes, or never remember the properties of the segments in triangles? Get that number closer to always with a creative lesson analyzing all four segments. Scholars consider a statement about one of the...
101 Questions
Canadian Thanksgiving Tradition
It's all about the portion size! Given a photo of a pumpkin pie, learners work to determine the number of calories that are missing. Supplemental information provides the angle of the piece that is missing as well as the nutritional...
Physics Classroom
Vector Direction
Scholars practice vector direction notation in multiple formats. After mastering each individually, they work to convert from one to another as one part in a series of lessons on vectors and projectiles.
101 Questions
Brita
It's hard to envision what 39 billion plastic bottles look like. Brita claims that the US uses that number of plastic bottles each year! If that's not enough to get your attention, figure out how many times 39 billion water bottles can...
101 Questions
Pool Capacity
Here's hoping that we can all fit into the pool. Given pictures and dimensions of a pool in tile lengths, scholars decide how many people can fit into the pool. This requires consideration of area, as well as the application of some...
101 Questions
Car Caravan
Keep playing with those old toy cars! Pupils estimate the number of toy cars in an art installation. The only information they receive is a picture showing the toy cars arranged in concentric rings and the diameter of the overall...
101 Questions
Lucky Cow
Cutting the cheese isn't a joke. Scholars observe a wedge of cheese and must determine how to cut it in half horizontally. They apply their knowledge of sectors to determine the most accurate way to slice the cheese.
101 Questions
Red Carpet
Roll out the red carpet for an exemplary lesson. Using the dimensions of a rolled piece of carpet, learners calculate the dimensions of the flat sample. Pictures provide individuals with the information they need to make a valid conclusion.
101 Questions
Penny Circle
Watch as your classes buy into a rich lesson full of information. A video opener challenges individuals to determine the number of pennies that fit in a circle with a 22-inch diameter. Using lesson materials, scholars collect data and...
101 Questions
Suitcase Circle
Analyze patterns in a circular arrangement. After using a geometric construction to complete a circle, learners use proportional reasoning to make predictions. By determining the length of an arc built from suitcases, they estimate the...
101 Questions
Rotonda West, FL
The shortest distance from point A to point B is a straight line—or is it? Young scholars determine the shortest route either along a circular path or through the center of the circle. Learners gain a unique perspective on arc length and...
101 Questions
Apple Mothership
Explore Apple's spaceship office building. Built in the shape of a circle, the office building offers a unique floor plan challenge. Young scholars use the dimensions of the building to estimate the square footage for each employee.
101 Questions
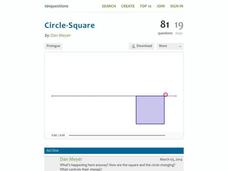
Circle-Square
How do the area and perimeters of circles and squares compare? A clever video illustrates the change in the area of a circle and square while their total perimeter stays the same. The task is for learners to predict the point where the...
101 Questions
Best Circle
Drawing the perfect circle is harder than one would think! What makes a circle a circle and how can you define that with a formula? Young mathematicians devise their own methods of analyzing the imperfections of circle drawings. Using...
Shodor Education Foundation
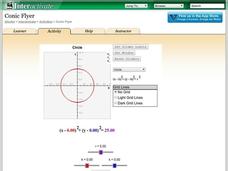
Conic Flyer
Graphing conics made easy. Individuals use an interactive to graph conic sections. The app can handle circles, vertical and horizontal parabolas, ellipses, and vertical and horizontal hyperbolas.
CK-12 Foundation
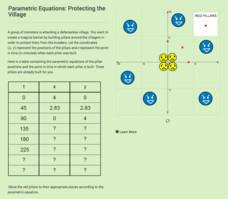
Parametric Equations: Protecting the Village
Determine the location of the pillars in time. Given a table of values for two parametric equations, pupils complete the table to determine the location and time it takes to build the pillars. Learners plot the points representing...
CK-12 Foundation
Circles Not Centered at the Origin: Room Rearranging
Where does a circular table fit best? Individuals move a circle representing a table into different quadrants of a room. Pupils determine which equation of the circle will place the table in the appropriate quadrant. A discussion...
CK-12 Foundation
Circles Centered at the Origin: Dog
How many bones can a dog on a leash reach? Class members move a dog on the end of its leash and determine whether it can reach bones located at specific points. The learners see whether the bone lies on the circle or outside of the...
CK-12 Foundation
Circles Centered at the Origin: The Map of the Beta Solar System
Calculate galactic orbits in a far-out resource. Pupils drag a point on a circle to graph the orbit of a fictional planet. Using the equation, they find points through which the orbit passes. To finish the simulation, users determine the...
CK-12 Foundation
Equations of Circles: Finding the Equation of a Circle
It's all about location and size. With the aid of the interactive, pupils explore the relationship between the location and size of a circle and its equation. The learners use that relationship to determine the equation of a circle given...
CK-12 Foundation
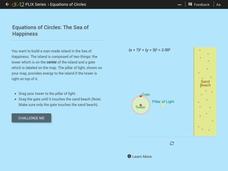
Equations of Circles: The Sea of Happiness
Map this! Help your young mathematicians draw a circular island on a map. Given specifics of the location and size of an island on a map, pupils transform a circle to meet the given requirements. They then determine the location of the...
CK-12 Foundation
Restricted Domain and Range: Restricted Circle Radius and Area
There's no restriction to how much your class can learn about domain and range. Users of an interactive adjust the radius of a circle to see its effects on the area. They note how restrictions in the domain (radius) relate to...
CK-12 Foundation
Algebraic Functions: Vertical Line Test
To be (a function) or not to be (a function). An easy-to-use interactive has pupils drag a vertical line onto several graphs to determine if they represent functions. Some challenge questions assess understanding of this idea.
CK-12 Foundation
Vertical Line Test: Exploration
What do vertical lines have to do with functions? Individuals slide a vertical line through four different graphs. They use that vertical line test to determine if the graphs represent functions.