CK-12 Foundation
Law of Cosines: Baseball Diamond
Catch a great resource! Individuals use an interactive that allows them to move players on a baseball field. They calculate distances between players using the Law of Cosines.
CK-12 Foundation
Law of Cosines: Get on Base
Baseball is all about math. Young baseball and mathematics enthusiasts determine the distance between players on a baseball field using the Law of Cosines. An interactive helps them find relevant distances and angles to use in their...
CK-12 Foundation
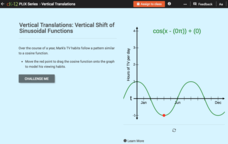
Vertical Translations: Vertical Shift of Sinusoidal Functions
Create a shift in TV viewing habits. The interactive presents a cosine model of an individual's TV viewing habits during a year. Class members move the model to reflect given conditions. Finally, they determine key features from the...
CK-12 Foundation
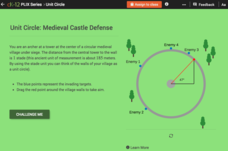
Unit Circle: Medieval Castle Defense
Who needs a plan — let trigonometry protect you! Pupils determine the angle of an approaching enemy to a village wall. The scholars determine the exact value of trigonometric functions for the angle. Class members use trigonometry to...
CK-12 Foundation
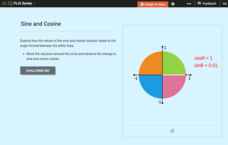
Domain, Range, and Signs of Trigonometric Functions: Sine and Cosine
Is there a relationship between the sign of sine and cosine and the angle on the unit circle? Scholars use an interactive to see the value of sine and cosine within different quadrants. they then use the information to determine the...
CK-12 Foundation
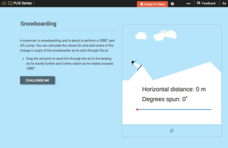
Trigonometric Functions of Angles Greater than 360 Degrees: Snowboarding
Spin through the trigonometric functions. Scholars determine the angle of rotation a snowboarding snowman makes at various distances in his jump. The class members then calculate the values of trigonometric functions for those angles.
CK-12 Foundation
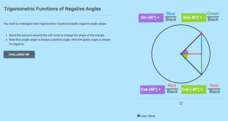
Trigonometric Functions of Negative Angles
When is the trigonometric value of a negative angle the same as the positive angle? Pupils compare the values of trigonometric functions for different angles and their negatives. The interactive resource provides a visual display to make...
CK-12 Foundation
Horizontal Translations or Phase Shifts: Cosine
If cosine is shifted, how is its equation affected? Learners manipulate the graph of cosine by moving the y-intercept to different locations on the coordinate plane. Pupils determine the new equation that models the shifts.
CK-12 Foundation
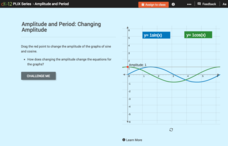
Sine Graph and Cosine Graph: Changing Amplitude
Scholars manipulate the amplitude of the graphs of sine and cosine, notice how the change in amplitude is reflected in their graphs, and answer several questions about the concept they noticed.
CK-12 Foundation
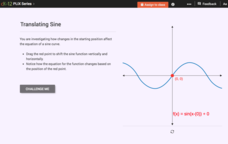
Translating Sine and Cosine Functions: Translating Sine
Learn how to slide sine back and forth and up and down. Pupils move the starting point of a graph of sine vertically and horizontally. They investigate the changes to the equation of the graph in relationship to the translation. They...
CK-12 Foundation
Reference Angles and Angles in the Unit Circle: Exploring Reference Angles
A steal of a deal — get four angles for the value of one. An interactive resource allows individuals to visualize all four angles that have the same reference angle. Pupils answer questions by using the interactive to create the...
CK-12 Foundation
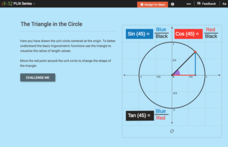
Trigonometric Functions and Angles of Rotation: The Triangle in the Circle
Go around the unit circle and create triangles. Pupils move a point around the unit circles to visualize the triangle associated with the angle in standard position. The three main trigonometric functions are defined in terms of the legs...
CK-12 Foundation
Sine, Cosine, and Tangent Functions: Lighthouse
How far is that boat from the lighthouse? Scholars create diagrams to represent a scenario given the angle of depreciation from a lighthouse to a boat. Learners apply the basic trigonometric functions to find various distances...
CK-12 Foundation
Basic Trigonometric Functions: Ladder Length
Climb the ladder to trigonometry. The interactive introduces trigonometric ratios and finding lengths of sides of right triangles created by a ladder and a building. Learners use the interactive to create triangles by moving the top of...
Virginia Department of Education
Special Right Triangles and Right Triangle Trigonometry
Right triangles are so special! Use special right triangles to discover the trigonometric ratios. Pairs construct special right triangles and find the values of the ratios of the sides. In the process, they discover the ratios stay the...
Illustrative Mathematics
Coordinates of Equilateral Triangles
Can it be constructed? The task poses the question whether it is possible to have an equilateral triangle with its vertices located at integer coordinates. Pupils work with their knowledge of trigonometric ratios and the Pythagorean...
EngageNY
Exploiting the Connection to Trigonometry 1
Class members use the powers of multiplication in the 19th installment of the 32-part unit has individuals to utilize what they know about the multiplication of complex numbers to calculate the integral powers of a complex...
West Contra Costa Unified School District
Introduction to Trigonometric Functions
Scholars first learn the definitions of the sine ratio, the cosine ratio, and the tangent ratio. After mastering these definitions, they use the new information to solve triangles.
EngageNY
What Is a Trigonometric Identity?
Protect yourself from identity theft! Establishing a strong understanding of the Pythagorean identity allows learners to prove that sine^2x + cos^2x = 1. They then use the identity to find sine or cosine ratios given the other.
EngageNY
Algebra II Module 2: Mid-Module Assessment
Time for classes to show what they've learned. Use several tasks to assess understanding of the trigonometric functions, unit circle, radians, and basic trigonometric identities.
EngageNY
Awkward! Who Chose the Number 360, Anyway?
Don't give your classes the third degree. Use radians instead! While working with degrees, learners find that they are not efficient and explore radians as an alternative. They convert between the two measures and use radians with the...
EngageNY
Graphing the Sine and Cosine Functions
Doing is more effective than watching. Learners use spaghetti to discover the relationship between the unit circle and the graph of the sine and cosine functions. As they measure lengths on the unit circle and transfer them to a...
EngageNY
Extending the Domain of Sine and Cosine to All Real Numbers
Round and round we go! Pupils use reference angles to evaluate common sine and cosine values of angles greater than 360 degrees. Once they have mastered the reference angle, learners repeat the process with negative angles.
EngageNY
From Circle-ometry to Trigonometry
Can you use triangles to create a circle? Learners develop the unit circle using right triangle trigonometry. They then use the unit circle to evaluate common sine and cosine values.