CK-12 Foundation
Division of Rational Expressions: Step by Step
Division just got a little trickier! An interactive lesson highlights the steps of dividing two rational expressions. Young scholars determine the order of the steps from a bank of possible work.
CK-12 Foundation
Using Quadratic Equations to Solve Problems: Construct a Soccer Field
Build a soccer field through a little mathematical analysis. Individuals manipulate the dimensions of a soccer field as they drag points to new positions. The simulation shows the corresponding intercepts and area. As pupils explore the...
CK-12 Foundation
Greatest Common Factor Using Lists: Tiling the Kitchen Floor
Use a combination of tiling a rectangle to find area and find the greatest common factor of the lengths of two sides and the area they create. Pupils increase and decrease the sides of the rectangle before answer five questions about...
CK-12 Foundation
Multiplication of Rational Expressions
There's nothing irrational about this lesson. Explore the process of multiplying rational expressions through discovery. A well-designed lesson has learners factor and multiply rational expressions by dragging factors to the correct place.
CK-12 Foundation
Negative Exponents
Watch the exponent expression do the negative exponent dance! An interactive lesson uses an animation to show how negative exponents become positive. Learners manipulate the expression and then respond to conceptual questions.
CK-12 Foundation
Inverse Variation Models: Speedometer for Inverse Variation Models
Model inverse variation while solving a real-world problem. Young scholars use the interactive lesson to discover the pattern of inverse variation data. They then use that discovery to write and analyze an equation.
CK-12 Foundation
Simplifying Rational Expressions: Sliding Solver
Build a strong understanding of simplified rational expression with your classes. An interactive lesson helps scholars discover the equality between the original expression and the simplified expression. Questions help individuals focus...
CK-12 Foundation
Solving Problems by Factoring: Building a Doghouse
Building a doghouse is easier with a little mathematical help! Young scholars use sliders to adjust the length of the doghouse and watch as it affects the width and area. They then answer questions that help them discover the question...
CK-12 Foundation
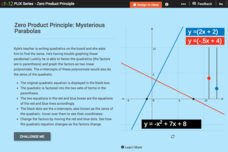
Zero Product Principle: Mysterious Parabolas
Be a hero, not a zero! Help your classes understand how to solve quadratic equations with the zero product property using an animated simulation. Using the controls, scholars manipulate the zeros and watch as the function and its factors...
CK-12 Foundation
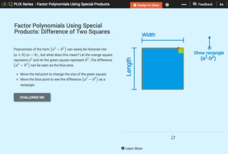
Factor Polynomials Using Special Products: Difference of Two Squares
Factoring patterns are not magic! Show your classes how to model the difference of two squares' factors using an area model. Learners manipulate the width and length of two squares to represent the polynomial a^2-b^2. They use the model...
CK-12 Foundation
Sum and Difference of Cubes: Stacking Blocks
Investigate polynomial factoring patterns by finding a connection to volume. As learners build a three-dimensional solid from smaller solids, they convert the visual model to a mathematical expression. Their models represent the sum of...
CK-12 Foundation
Factoring by Grouping: Polynomials
Investigate the process of factoring polynomials by grouping. A detailed lesson initially has learners follow a set-by-step example. They then drag terms to complete the three steps of a new problem.
CK-12 Foundation
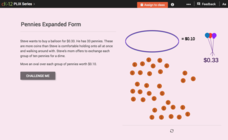
Numbers in Expanded Form: Pennies Expanded Form
Beginning with a word problem that poses the question of making groups of 10 pennies to translate into a single dime, pupils are challenged to make sense of the amount of dollars 33 cents is in expanded form.
CK-12 Foundation
Equivalent Fractions: Number Line
Arrange improper fractions on a number line to determine the equivalency to whole numbers. The number line starts at -4 and ends at 4, while users must turn the improper fraction into a proper fraction in order to place it on the number...
CK-12 Foundation
Pythagorean Theorem to Determine Distance: Neighborhood Map
Find the distance between various locations in a neighborhood. Scholars use the interactive to find distances between locations on a map. The map is overlaid onto a grid to provide coordinates for each location, and pupils apply...
CK-12 Foundation
Pythagorean Theorem to Determine Distance: Distance Between Friends
Pupils use an interactive to help visualize the right triangles needed to calculate distances between friends' houses. Individuals solve five problems on how to determine distances and comparing the distances.
CK-12 Foundation
Special Triangle Ratios: Special Right Triangle Ratios
Go from one side length to any other side length with special right triangles. Individuals use the interactive to investigate the ratio of sides in 45-45 and 30-60 right triangles. Scholars make generalizations about the types of special...
CK-12 Foundation
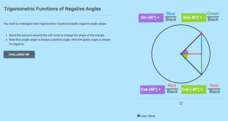
Trigonometric Functions of Negative Angles
When is the trigonometric value of a negative angle the same as the positive angle? Pupils compare the values of trigonometric functions for different angles and their negatives. The interactive resource provides a visual display to make...
CK-12 Foundation
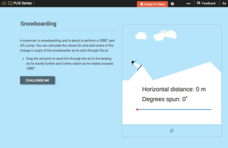
Trigonometric Functions of Angles Greater than 360 Degrees: Snowboarding
Spin through the trigonometric functions. Scholars determine the angle of rotation a snowboarding snowman makes at various distances in his jump. The class members then calculate the values of trigonometric functions for those angles.
CK-12 Foundation
Reciprocal Identities
Get a better understanding of the trigonometric functions by taking a look at the flip side. Pupils create angles within a unit circle and compare the values of the standard trigonometric functions to their reciprocal functions. The...
CK-12 Foundation
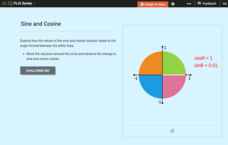
Domain, Range, and Signs of Trigonometric Functions: Sine and Cosine
Is there a relationship between the sign of sine and cosine and the angle on the unit circle? Scholars use an interactive to see the value of sine and cosine within different quadrants. they then use the information to determine the...
CK-12 Foundation
Conversion between Degrees and Radians: Clock Angles and Measures
It's 3:30, what radian is it? Pupils create clock angles on a clock and determine the radian measure to the minute hand. They then use a conversion factor to convert from one measurement to another.
CK-12 Foundation
Six Trigonometric Functions and Radians: Degrees to Radians and Back Again!
How do degrees relate to radians? The interactive allows pupils to manipulate the size of an angle in a unit circle to help see that relationship. Users determine the radian measure for given degree measures of angles, realizing the...
CK-12 Foundation
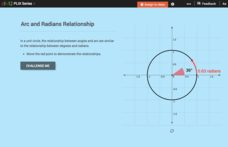
Conversion between Degrees and Radians: Arc and Radians Relationship
How are arc lengths and radians related? An interactive resource demonstrates the relationship as pupils create arc lengths in a unit circle and compare them to the angle measurements. Questions ask individuals to build upon this...
Other popular searches
- New Years Resolutions
- New Year Resolutions
- Debate Resolutions
- New Year's Resolutions
- Poetry New Year Resolutions
- United Nations Resolutions
- Resolutions for New Year
- Positive Resolutions
- Writing Resolutions
- Conflict Resolutions
- Making New Years Resolutions
- New Year Resolutions Poems