CK-12 Foundation
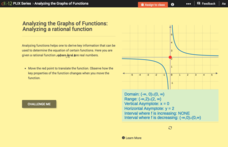
Analyzing the Graphs of Functions: Analyzing a Rational Function
Shift the function and transform the key features of the graph. By translating the graph of the rational function, class members find out how the key features alter. Pupils determine the domain, range, asymptotes, and intervals of...
CK-12 Foundation
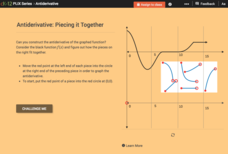
Antiderivative: Piecing it Together
Build a function backwards. Given a graph of the derivative of a function, pupils piece together a graph of the original function, the antiderivative. Learners use their graphs and the graphs of the derivatives to answer questions about...
CK-12 Foundation
Continuity at a Point, Continuity Test, Types of Discontinuity: Properties of Continuous Functions
Take a closer look at continuous functions within given intervals. Using the parent cubic function, learners explore properties of continuous functions on intervals. Pupils interpret the Intermediate Value Theorem and the Extreme Value...
CK-12 Foundation
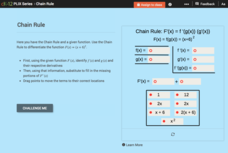
Chain Rule
Keep it on the chains. Pupils work through the steps in the chain rule using the interactive as a guide. Learners identify the two composed functions and their associated derivatives from a set of choices. They continue on to build the...
CK-12 Foundation
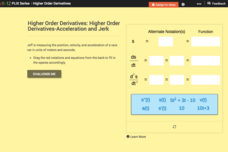
Higher Order Derivatives—Acceleration and Jerk
Accelerate your class through finding the second derivative. Using a bank of equations, pupils determine the equations for distance, velocity, and acceleration and their associated function notations. With the equations, learners answer...
CK-12 Foundation
Related Rates of Car Speeds
Speed up your pupils' understanding of derivatives. Two cars travel in perpendicular distances to each other. With the aid of the interactive, learners visualize the situation. Pupils use the derivative to calculate the instantaneous...
CK-12 Foundation
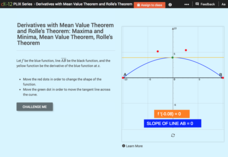
Derivatives with Mean Value Theorem and Rolle's Theorem: Maxima and Minima
Rolle with the mean values and derivatives. Scholars complete the statements of Rolle's Theorem and the Mean Value Theorem. Using the interactive to illustrate scenarios, pupils respond to questions concerning the theorems in terms of...
CK-12 Foundation
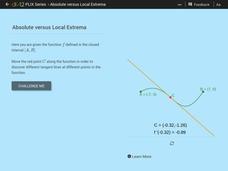
Absolute Versus Local Extrema
Get the class to take an extreme look at functions. The interactive presents a function on a closed interval with a movable tangent line. Using the given function, pupils determine the extrema, critical points, and points of...
CK-12 Foundation
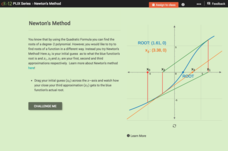
Newton's Method
Does the accuracy of the first guess make a difference down the line? Learners investigate the effects of the iterative process of finding roots, using Newton's Method. By moving the initial guess of a root on a graph, pupils observe the...
CK-12 Foundation
Intermediate Value Theorem, Existence of Solutions: Function Exploration
Does the value exist? The interactive allows pupils to visualize the Intermediate Value Theorem. Using the visualization, individuals respond to questions using specific values and general values. The class comes to the conclusion what...
CK-12 Foundation
Average and Instantaneous Rates of Change
How can you determine the rate of change on a curve? Pupils use the interactive to discover what happens with the average rate of change as the point move closer to the other. Using the definition of the derivative, learners find that it...
CK-12 Foundation
Tangent Line Approximation: Estimating Square Roots
Estimating a square root is as easy as evaluating a linear equation. Using the derivative of the square root function, pupils calculate an estimation of square roots. Class members determine the equation of the tangent line at the value...
CK-12 Foundation
Derivatives of Trigonometric Functions: Derivative of sin(x)
Graphically find the derivative of sin(x). Using the interactive, pupils graph the slope of the tangent line to the sine function. Class members use the resulting graph to determine the derivative of the sine function. They verify their...
CK-12 Foundation
Absolute Extrema and Optimization: Building the Biggest Box
Optimally, you want the largest box. Given a square piece of box material, pupils determine the size of congruent squares to cut out of the corners to create a box with the greatest volume. Learners determine the equation of the volume...
CK-12 Foundation
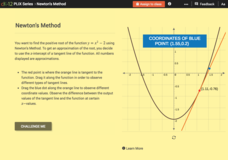
Newton's Method
Use an iterative process to find an approximation of a square root. Pupils use the interactive to find an approximation to find the positive root of a quadratic function with Newton's method. With the graphs, learners position the...
CK-12 Foundation
Area Sums: Estimation with Rectangles
The more rectangles, the better the estimate. Using the interactive, pupils explore estimating the area under a curve using left-hand sums. Learners respond to challenge questions on how to get better estimates using the same technique.
CK-12 Foundation
Properties of Definite Integrals
Close your eyes and visualize a definite integral. An interactive provides a visualization of a function and definite integral on a closed interval. Pupils move one point of the interval in either the positive or negative direction....
CK-12 Foundation
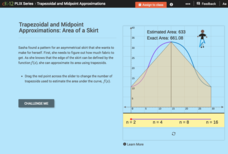
Trapezoidal and Midpoint Approximations: Area of a Skirt
When are trapezoids better than rectangles? Using trapezoids pupils approximate the area of fabric defined by a function. Just like with rectangles, learners realize the more trapezoids the more accurate the approximation. Scholars use...
CK-12 Foundation
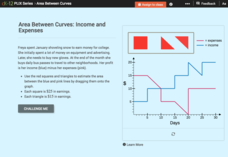
Area Between Curves: Income and Expenses
Use the area of polygons to calculate the area between curves. Pupils calculate areas under income and expense curves by filling the space with squares and right triangles. Using that information, they determine the profit related to the...
CK-12 Foundation
Method of Cylindrical Shells
Approximate the volume of a solid of revolution. Using a method similar to approximating the area under a curve, pupils investigate the volume of a solid of revolution. The learners use a given definite integral to find the volume of...
CK-12 Foundation
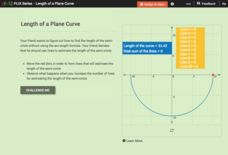
Length of a Plane Curve
Challenge your class to use straight lines when estimating the length of a curve. An engaging interactive allows individuals to place line segments one after another along the arc. Learners determine that the more lines used, the better...
CK-12 Foundation
Work and Force: Lifting a Bucket
How much work does it take to lift a bucket? An interactive presents a problem of lifting a bucket from the ground to the top of a building. Using their knowledge about work and integrals, pupils calculate the amount of work required to...
CK-12 Foundation
Differential Equations Representing Growth and Decay: Rice Legend
The legend of a wise man who asks a king for rice as a reward presents a context to study exponential solutions to differential equations. Pupils move quantities of rice to a chessboard and calculate the amount of rice for each day. To...
CK-12 Foundation
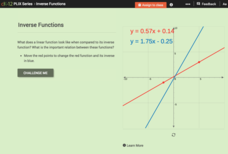
Inverse Functions
Provide a graphical view of inverses. Pupils manipulate points on a line and see the relationship of the graph with the graph of its inverse. Using the relationship between the graphs, scholars respond to questions concerning inverses...