Teach Engineering
Can You Resist This?
Some things are hard to resist. Small collaborative groups build circuits and calculate the voltage using Ohm's Law. Budding engineers explore the connection between the voltage across different resistors and linear functions with...
Inside Mathematics
Archery
Put the better archer in a box. The performance task has pupils compare the performance of two archers using box-and-whisker plots. The resource includes sample responses that are useful in comparing individuals' work to others.
Inside Mathematics
Conference Tables
Pupils analyze a pattern of conference tables to determine the number of tables needed and the number of people that can be seated for a given size. Individuals develop general formulas for the two growing number patterns and use them to...
EngageNY
Association Between Categorical Variables
Investigate associations between variables with two-way tables. Scholars continue their study of two-way tables and categorical variables in the 15th installment of a 21-part module. The lesson challenges them to calculate relative...
Noyce Foundation
Gym
Give the class a mental work out with an assessment task in which young mathematicians compare several gym membership options. They use substitution to calculate the cost for given numbers of months.
Noyce Foundation
Percent Cards
Explore different representations of numbers. Scholars convert between fractions, decimals, and percents, and then use these conversions to plot the values on a horizontal number line.
EngageNY
Graphs of Linear Functions and Rate of Change
Discover an important property of linear functions. Learners use the slope formula to calculate the rates of change of linear functions. They find that linear functions have constant rates of change and use this property to determine if...
Virginia Department of Education
Normal Distributions
Pupils work to find probabilities by using areas under the normal curve. Groups work to calculate z-scores and solve real-world problems using the empirical rule or tables.
Cornell University
Math Is Malleable?
Learn about polymers while playing with shrinky dinks. Young scholars create a shrinky dink design, bake it, and then record the area, volume, and thickness over time. They model the data using a graph and highlight the key features of...
Teach Engineering
Start Networking!
Class members create their own social networks by collecting signatures before graphing the interactions with their fellow classmates. The degree distribution of the simulated social network is determined by calculating the degree of...
Virginia Department of Education
Factoring
Uncover the relationship between factoring quadratics and higher degree polynomials. Learners develop their factoring skills through repetition. A comprehensive lesson begins with quadratics and shows how to use the same patterns to...
College Board
2005 AP® Calculus AB Free-Response Questions
Develop an awareness of the exam. Pupils and teachers use the six release free-response questions to see how the exam covers topics. The questions are divided among calculator and non-calculator items. Scholars see the importance of...
Curated OER
Everyday Math Experiences
Students can put away the workbooks and experience a real world math day.
Teach Engineering
Household Energy Audit
Do you have an energy hog in your home? Individuals pick at least one room at home to determine the amount of energy the appliances consume. Using that information, pupils fill out a worksheet to determine the cost of running each...
Curated OER
Candy Machine
Using the concept of a candy vending machine, young mathematicians explore the sugar ratios found in different types of candy. Using the provided information, class members calculate and compare different ratios in order to find the...
Inside Mathematics
How Old Are They?
Here is a (great) lesson on using parentheses! The task requires the expression of ages using algebraic expressions, including the distributive property. Pupils use their expressions to determine the individual ages.
Inside Mathematics
Quadrilaterals
What figure is formed by connecting the midpoints of the sides of a quadrilateral? The geometry assessment task has class members work through the process of determining the figure inscribed in a quadrilateral. Pupils use geometric...
EngageNY
Volumes of Familiar Solids – Cones and Cylinders
Investigate the volume of cones and cylinders. Scholars develop formulas for the volume of cones and cylinders in the 10th lesson of the module. They then use their formulas to calculate volume.
EngageNY
Distance on the Coordinate Plane
Apply the Pythagorean Theorem to coordinate geometry. Learners find the distance between two points on a coordinate plane by using the Pythagorean Theorem. The vertical and horizontal change creates a right triangle, which allows...
EngageNY
Estimating a Population Proportion
Find the percent of middle schoolers who want the ability to freeze time. The 21st installment in a series of 25 has groups collect a random sample of respondents who answer a question about superpowers. Using sample statistics,...
EngageNY
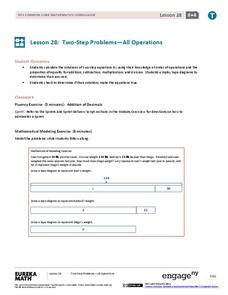
Two-Step Problems—All Operations
Step 1: Use the resource. Step 2: Watch your class become experts in solving two-step problems. Scholars learn to solve two-step word problems in context. They use tape diagrams and algebraic techniques to break the problem into two,...
Noyce Foundation
Rabbit Costumes
How many rabbit costumes can be made? This is the focus question of an activity that requires scholars to use multiplication and division of fractions to solve a real-world problem. They determine the amount of fabric necessary for eight...
EngageNY
End-of-Module Assessment Task: Grade 7 Mathematics Module 6
Determine the level of understanding within your classes using a summative assessment. As the final lesson in a 29-part module, the goal is to assess the topics addressed during the unit. Concepts range from linear angle relationships,...
EngageNY
The Difference Between Theoretical Probabilities and Estimated Probabilities
Flip a coin to determine whether the probability of heads is one-half. Pupils use simulated data to find the experimental probability of flipping a coin. Participants compare the long run relative frequency with the known theoretical...