EngageNY
The Definition of a Parabola
Put together the pieces and model a parabola. Learners work through several examples to develop an understanding of a parabola graphically and algebraically.
Texas Instruments
Properties of Parabolas
Explore the properties of parabolas in this lesson. Construct a parabola given a focus and a directrix on the Ti-Nspire. Write equations of parabolas in vertex form and determine the a value of a parabola given a focus and directrix.
Curated OER
Properties of Parabolas
Learn to identify the properties of parabolas. Students define parabola as the locus of all points equidistant from a fixed point and a fixed line. Also, interpret the equation for a parabola in vertex form and gain a visual...
Curated OER
Exploring Geometric Constructions of Parabolas
Students are introduced to the construction geometrically of parabolas. Using a software program, they identify lines, segments and midpoints. They label the parabolas properties and characteristics and use a formula to determine the...
Curated OER
Using the Distance Formula
In this distance formula learning exercise, students solve and complete 30 various types of problems. First, they find the exact distance between each pair of points and make a sketch of the situation. Then, students find the center,...
Curated OER
Parabolas
Students review the definition of a parabola. They trace a parabola by locating points the same distance from a point as they are to a line. Students develop an equation for a parabola with its vertex at the origin. Students solve...
Curated OER
Introduction to Conic Sections
Learners slice cones and identify the different conics formed. They then derive the formula to solve problems involving cones. Pull out the TI calculators to visualize the slicing and the different parts and properties created.
Texas Instruments
Texas Instruments: Conics as a Locus of Points
Students investigate the definition of a parabola through one of its geometric definitions. They study conic sections. They examine an ellipse as a locus of points such that the sum of distances from the foci to the traced path is constant.
Math Open Reference
Math Open Reference: Parabola
Learn about the three ways to define a parabola: Focus and Directrix, The Graph of a Function, and As a Conic Section. Examples are provided.
Other
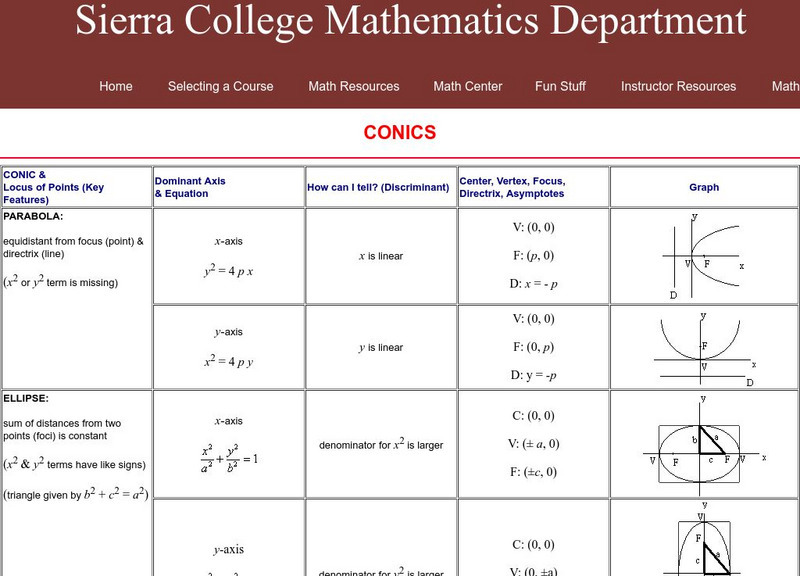
Sierra College: Conics
Provides the locus of points, dominant axis and equation, discriminant, center, vertex, focus, directrix, and asymptotes for the parabola, the ellipse, and the hyperbola.
Other
Platonic Realms: Conics
This resource provides in depth information on the conic sections. Click on the underlined words for definitions and diagrams.