Curated OER
A.P. Calculus Integration Test
In this A.P. Calculus worksheet, students complete a sixteen question test covering trigonometric integration, area under a curve, differential equations, and slope fields. Some of the problems are multiple choice, while others are...
Curated OER
Integrals and Integration
In this calculus activity, students evaluate definite integrals using numbers and radians. They take the derivative to solve their equations, using trigonometric identities. There are 4 questions.
Curated OER
Integrals
In this integrals worksheet, learners solve and complete 22 various types of problems. First, they evaluate each of the listed integrals by using substitution. Then, students solve each of the given differential equations when given the...
Curated OER
The Integration of Exponential Functions
In this calculus learning exercise, students solve problems using integration. They solve exponential functions using differentiation formulas. There are 12 problems with an answer key.
Curated OER
The Method of Integration by Parts
In this calculus worksheet, students perform integration by parts. They solve differential equations as they use integration by part to solve unlike terms. There are 23 problems with an answer key.
Curated OER
The Limit Definition of a Definite Integral
In this calculus worksheet, learners calculate the derivative and integral of different functions. They use interval to mark the beginning and end of their calculations. There are 15 questions with an answer key.
Curated OER
The Method of Integration by Partial Fractions
In this calculus worksheet, students solve problems using integration by partial fractions. They add fractions to get a common denominator, then take the derivative. There are 20 questions with an answer key.
Curated OER
Proof That One Equals Zero (Using Calculus)
In this proofs worksheet, learners evaluate the integral of 1 function. Students use uv-substitution to prove 0=1.
Curated OER
Setting Up Definite Integrals Using Local Approximations First
In this math worksheet, students practice solving the problems concerning the use of integrals. They focus upon using local approximations first for the word problems.
CK-12 Foundation
Volume by Disks: The Vase Case
Finding the volume is an integral characteristic of a vase. Using the idea that summing the areas of cross-sectional disks will calculate the volume of a rotational solid, pupils find the volume of a vase. Scholars determine the interval...
CK-12 Foundation
Work and Force: Lifting a Bucket
How much work does it take to lift a bucket? An interactive presents a problem of lifting a bucket from the ground to the top of a building. Using their knowledge about work and integrals, pupils calculate the amount of work required to...
CK-12 Foundation
Method of Cylindrical Shells
Approximate the volume of a solid of revolution. Using a method similar to approximating the area under a curve, pupils investigate the volume of a solid of revolution. The learners use a given definite integral to find the volume of...
College Board
2001 AP® Calculus BC Free-Response Questions
Take an abbreviated look at the exam. Class members review released items to prepare for the BC exam. The released questions are the six free-response questions from the 2001 exam. Three of the items have context, while the other three...
CK-12 Foundation
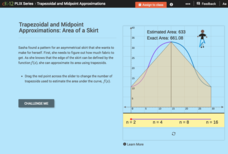
Trapezoidal and Midpoint Approximations: Area of a Skirt
When are trapezoids better than rectangles? Using trapezoids pupils approximate the area of fabric defined by a function. Just like with rectangles, learners realize the more trapezoids the more accurate the approximation. Scholars use...
Flipped Math
Calculus AB/BC - Particular Solutions using Initial Conditions and Separation of Variables
Take the next step in separating. Pupils pick up from the previous lesson to now find the particular solution of a differential equation at a given point. Scholars watch three examples of finding the particular solution and hear the...
Curated OER
Passive Integrator and Differentiator Circuits
In this circuits worksheet, students answer 25 questions about passive integrator circuits and passive differentiator circuits given schematics showing voltage. Students use calculus to solve the problems.
Curated OER
Exploring Functions with Calculus and Dynamic Software
Calculus can be project-based and inquiry-centered by using dynamic software.
College Board
Approximation
Sometimes close enough is appropriate. A curriculum document for AP® Calculus examines the importance of providing approximation questions throughout the course. It looks at approximating derivative values, approximating definite...
Texas Instruments
Sands of Time
Twelfth graders explore an application of integration. A calculus lesson prompts class members to find the length of the day where they live during the winter and summer solstice. Using data relating to the solstices at various...
CK-12 Foundation
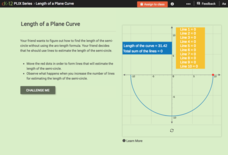
Length of a Plane Curve
Challenge your class to use straight lines when estimating the length of a curve. An engaging interactive allows individuals to place line segments one after another along the arc. Learners determine that the more lines used, the better...
Curated OER
The Method of U-Substitution
In this calculus worksheet, students solve problems using U-Substitution. They find antiderivatives using indefinite integrals. There are 18 questions with an answer key.
Curated OER
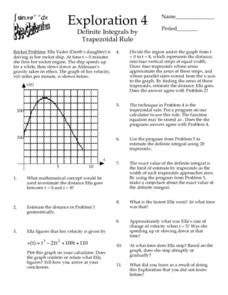
Exploration 4: Definite Integrals by Trapezoidal Rule
In this integral worksheet, students geometrically estimate distance in given problems. They use the trapezoidal rule to determine definite integrals. Students explore distance and velocity. This three-page worksheet contains...
Curated OER
Piecewise Linear Integral
Young mathematicians solve and graph piecewise functions in this calculus lesson. They integrate linear functions containing restrictions and graph their answers using the TI.
Curated OER
The Fundamental Theorem of Calculus and Properties of the Definite Integral
Young scholars discuss the importance of fundamental theorems in math. In this calculus lesson, students define the fundamental theorem of calculus and discuss why it is so important they understand it. They work problems to model how...