101 Questions
Gas Light
You don't want to leave any learners stranded! Explore ratios using an analysis of gas mileage and distance. Given a scenario, individuals must determine if a car has enough gas to make it to the next gas stop.
101 Questions
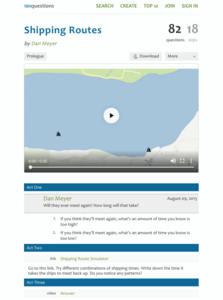
Shipping Routes
The product of the hard work is learning. Scholars use a simulation tool to collect information to analyze. They must decide when two ships traveling back and forth across a river at different rates will meet on the same side. The intent...
101 Questions
Sticky Stickies
Don't let your classes get stuck on area calculations—grab their attention with an inquiry-based lesson! Scholars must develop a plan to determine how may sticky notes it takes to cover the surface of a door. They decide on the...
101 Questions
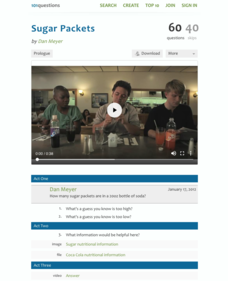
Sugar Packets
Depending on your eating habits, you just may not want to know the answer to the inquiry-based question! The task is to determine the number of sugar packets in one 20-ounce soda. Learners use nutritional information from the sugar and...
101 Questions
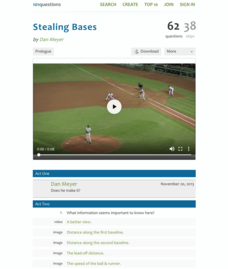
Stealing Bases
And he's ... safe? ... out? It's up to your scholars to decide! Provided with the speed of the runner and ball, learners develop a plan to determine which reaches the base first, the ball or the runner. While the distance from home to...
101 Questions
Canadian Thanksgiving Tradition
It's all about the portion size! Given a photo of a pumpkin pie, learners work to determine the number of calories that are missing. Supplemental information provides the angle of the piece that is missing as well as the nutritional...
101 Questions
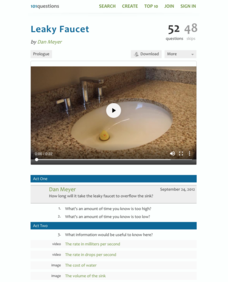
Leaky Faucet
A dripping faucet may be enough to drive you crazy, but it also teaches you a little about ratios. Presented with the volume of a sink and the rate the water is dripping, scholars must devise a plant to determine how long it will take...
101 Questions
Combining Coupons
Everyone likes to save money! Use your math skills to figure out just how much you can save on a pair of sweet shoes. A vendor is running a percent off sale, with a percent off coupon, and a specific dollar amount coupon—and lets you use...
101 Questions
Slow Church
The church that just can't stay put! A video presentation raises questions of just how far the church will move. Presented with the rate of movement and a range of time expected, scholars build an inequality to answer the question.
101 Questions
Ants Marching
Your classroom will be rockin' during an toe-tapping lesson! Dave Matthews inspires a lesson on proportions as youth listen to a song and predict its length. Lesson materials provide learners with ordered pairs that mark the time slider...
101 Questions
Brita
It's hard to envision what 39 billion plastic bottles look like. Brita claims that the US uses that number of plastic bottles each year! If that's not enough to get your attention, figure out how many times 39 billion water bottles can...
101 Questions
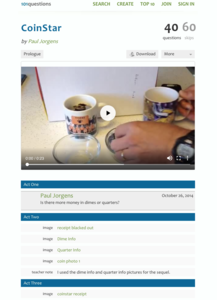
CoinStar
Would you rather have a bowl of dimes or a bowl of quarters? A video introduces the problem by presenting two bowls, one full of quarters and another full of dimes. Learners use information from a CoinStar receipt to calculate the number...
101 Questions
Pyramid of Pennies
Go big or go home! Learners watch a video rendition of the creation of a penny pyramid. Their task is to determine the number of pennies in the pyramid. The lesson encourages multiple methods, including function building or volume formulas.
101 Questions
Will It Hit The Hoop?
Basketball and math go hand in hand, even before one considers creating statistics. Viewers see a basketball player attempt multiple shots, but they do not see whether it goes in. They solve for which shots earned points as well as which...
101 Questions
Falling Glowsticks
How can you determine the height of a drop off a cliff if you have nothing to measure it with? A movie clip sets up a sky-high challenge and solves it with a falling glow stick. Scholars must take the given information and decide how...
101 Questions
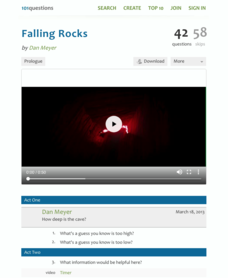
Falling Rocks
Can you determine how far down a rock drops without visual clues? Viewers observe a clip from a movie testing vertical distance only based on sound. They must determine if it is safe to drop down themselves or if it is farther than their...
101 Questions
Lunch
Traditional lamian, a noodle originating from China, is hand shaped by twisting, stretching, and folding the dough into strands. Scholars observe the technique before determining the length of the final noodle. They use exponential...
101 Questions
Money Duck
A video presentation shows duck-shaped soap that has a $1, $5, $10, $20, or $50 bill in its center. Learners consider different population distribution of the bills to determine a reasonable price for the duck.
101 Questions
Split Time
Stay on track to learn about proportions. Scholars watch an introductory video that shows the split time for a runner on an outdoor track. Applying concepts of proportional reasoning, they determine what the runner's split time would be...
101 Questions
Pool Capacity
Here's hoping that we can all fit into the pool. Given pictures and dimensions of a pool in tile lengths, scholars decide how many people can fit into the pool. This requires consideration of area, as well as the application of some...
101 Questions
Candle Eyes
Candlelight is in the eye of the distant beholder. Scholars first watch a video clip of a commercial claiming that the human eye can see candlelight from 10 miles away. They use this information to calculate how far we can see...
101 Questions
Woody's Raise
You want to be where everyone gets a raise. A short clip from the TV show Cheers provides the context for the task. After watching an interaction between a bartender and an owner regarding a raise, viewers write inequalities to represent...
101 Questions
Lightning then Thunder
Conquer your fear of thunder and proportions. After viewing a video of lightning and thunder, scholars consider how far away the storm is from the recorder. This obviously requires the use of proportions and rates.
101 Questions
Snail's Pace
Time doesn't fly when you're watching a snail cross a sidewalk. Combining the concepts of the Pythagorean Theorem and the distance, rate, and time formula, learners determine how long it takes a snail to go from one corner of a sidewalk...