Annenberg Foundation
Geometry 3D Shapes: Surface Area and Volume
Whether you wrap it or fill it, you're using geometric concepts. Classmates use an interactive approach to learn how to find volume and surface area of cylinders and prisms in the second lesson in a five-part series. The online lesson...
101 Questions
You Pour, I Choose
Tall and skinny or short and stout, which glass hold the most liquid? Learners analyze dimensions of cylindrical glasses to determine the one holding the greatest amount of liquid. They brainstorm the relevant dimensions before making...
101 Questions
Meatballs
Your classroom will overflow with learning as they analyze the volume in a pot of meatballs. Young mathematicians predict the number of meatballs that will make a pot of sauce overflow. They incorporate both the volume of cylinders and...
101 Questions
Hot Coffee
Your classes will be wide awake during a piping hot lesson! Introduce the resource with a video of the world-record-breaking cup of coffee. Learners work to determine the volume of the cup of coffee to predict if it will break the record.
CK-12 Foundation
Volume by Disks: The Vase Case
Finding the volume is an integral characteristic of a vase. Using the idea that summing the areas of cross-sectional disks will calculate the volume of a rotational solid, pupils find the volume of a vase. Scholars determine the interval...
CK-12 Foundation
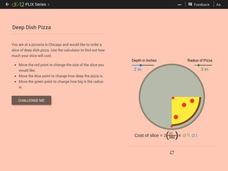
Linear Equations: Deep Dish Pizza
Explore the volume of solids with a real-life connection. Learners calculate the volume of a deep-dish slice of pizza to determine its price. They model the slice as a part of a cylinder and create a formula for calculating the cost.
Virginia Department of Education
Surface Area and Volume of a Cylinder
Surface area or volume? Pupils first review the difference between surface area and volume. They then use a two-dimensional net that helps them develop formulas for the surface area and volume of cylinders.
Virginia Department of Education
Surface Area and Volume
Partners use materials to wrap three-dimensional objects to determine the formula for surface area. The groups use an orange to calculate the amount of peel it takes to completely cover the fruit. Using manipulatives, individuals then...
EngageNY
End-of-Module Assessment Task: Grade 8 Mathematics (Module 7)
It's time to discover what your classes have learned! The final lesson in the 25-part module is an assessment that covers the Pythagorean Theorem. Application of the theorem includes distance between points, the volume of...
EngageNY
Volume of Composite Solids
Take finding volume of 3-D figures to the next level. In the 22nd lesson of the series, learners find the volume of composite solids. The lesson the asks them to deconstruct the composites into familiar figures and use volume formulas.
EngageNY
End-of-Module Assessment Task: Grade 8 Module 5
Give your class a chance to show how much they've learned in the module with an end-of-module assessment task that covers all topics from the module including linear and non-linear functions and volumes of cones, cylinders, and...
EngageNY
Volumes of Familiar Solids – Cones and Cylinders
Investigate the volume of cones and cylinders. Scholars develop formulas for the volume of cones and cylinders in the 10th lesson of the module. They then use their formulas to calculate volume.
Balanced Assessment
Boring a Bead
How much material is in a bead? Class members utilize volume formulas to determine the amount of material in a bead. The goal of the assessment is to show that the amount of material left in a bead is the same for all beads with a...
Mathematics Vision Project
Module 5: Modeling with Geometry
Solids come in many shapes and sizes. Using geometry, scholars create two-dimensional cross-sections of various three-dimensional objects. They develop the lesson further by finding the volume of solids. The module then shifts...
Mathematics Assessment Project
Calculating Volumes of Compound Objects
After determining the volume of various drinking glasses , class members evaluate sample responses to the same task to identify errors in reasoning.
Mathematics Assessment Project
Modeling: Making Matchsticks
Math: The only subject where the solution to a problem is seven million matches. Young scholars first complete an assessment task estimating the number of matches they can make from a tree of given dimensions. They then evaluate provided...
Mathematics Assessment Project
Glasses
Clink, clink! Young mathematicians investigate drinking glasses composed of known solids (cones, cylinders, and hemispheres). Next, they determine the volumes of these glasses.
Mathematics Assessment Project
Funsize Cans
Designing fun-size cans ... what fun! Class members use the provided questions to determine the dimensions of a can with a minimum surface area for a given volume. The task allows learners to use graphs or algebraic manipulation to...
Mathematics Assessment Project
Propane Tanks
As an assessment task, learners must determine the radius of a new tank that has double the capacity of a given tank. Task tests knowledge of determining volumes of cylinders and spheres.
Mathematics Assessment Project
Bestsize Cans
Traditional calculus problem made simple. In the high school assessment task, learners determine the minimum surface area for a can of a given volume using algebraic and numerical methods to solve the problem. No calculus...
University of Utah
Integer Exponents, Scientific Notation and Volume
A one-stop resource for exponents, square and cube roots, scientific notation, and volume formulas guides learners through properties of exponents. As they learn to apply these properties to operations with scientific notation,...
Charleston School District
Volume of Rounded Objects
How much can different shapes hold? The answer varies depending on the shape and dimensions. Individuals learn the formulas for the volume of a sphere, cone, and cylinder. They apply the formulas to find the volume of these...
Charleston School District
Review Unit 8: Geometry Applicaitons
Pupils complete a review worksheet that highlights the key problems from the first eight lessons in the series. Topics include the Pythagorean Theorem and its converse, as well as finding volume of three-dimensional figures.
Charleston School District
Solving for a Missing Dimension
If a can has a volume of twelve ounces, how tall it should be? If you can work with volume formulas, it's is an easy measurement to find. After finding the volume of figures in the previous lesson of the series, learners now...