Texas Instruments
Texas Instruments: Exploring the Vertex Form of the Quadratic Function
Students explore the vertex form of the parabola and discover how the vertex, direction, and width of the parabola can be determined by studying the parameters. They predict the location of the vertex of a parabola expressed in vertex form.
Texas Instruments
Texas Instruments: Investigating the Parabola in Vertex Form (Y = Ax2
In this activity, students investigate the standard form of the quadratic function, y = ax^2 + bx + c. They investigate the changes on the graph of a quadratic equation that result from changes in A, B, and C. They also locate the vertex...
Texas Instruments
Texas Instruments: Parabolic Applications
Students will analyze a parabola graphed from word problems. Students can use the calculator to find the roots and vertex of the graph to answer questions based on the word problems.
Texas Instruments
Texas Instruments: Prehistoric Parabola Match
This activity center is used as a formative assessment after a full unit on the different transformations of vertical parabolas.
Texas Instruments
Texas Instruments: Zeros of a Parabola
Students are introduced to an interesting property of parabolas and a method of proving that property using the TI-89 scripts. They then use the CAS of their TI-89 to generalize upon specific results.
Texas Instruments
Texas Instruments: Given a Graph, What Is the Function?
Understanding how to associate a function of a parabola with its graph. Students will explore varies functions and determine its graph. They will then use what they learned to predicate where a particular graph of a different function...
Texas Instruments
Texas Instruments: Standard Form of a Parabola
This activity will help students work with the standard form of a parabola y = a(x - h)^2 + k by writing an equation given the vertex and a point.
Texas Instruments
Texas Instruments: Quadratic Equations With the Cbl 2
Students will generate parabolas using the motion sensor. They will then determine the vertex form of the equation and compare it to the regression equation from the calculator.
Texas Instruments
Texas Instruments: Cutting Corners
Students' will continue to develop the idea of quadratic equations and parabolas.
Texas Instruments
Texas Instruments: Exploring the Width of a Parabola
Use TI-Navigator to explore the width of a parabola. All directions are provided on the teacher's guide.
Texas Instruments
Texas Instruments: Conics as a Locus of Points
Students investigate the definition of a parabola through one of its geometric definitions. They study conic sections. They examine an ellipse as a locus of points such that the sum of distances from the foci to the traced path is constant.
Texas Instruments
Texas Instruments: Exploring Transformations of the Quadratic Function
Using TI-Interactive, students will discover how the variables of a, h, and k in the vertex form of a quadratic function affect the size, shape and location of the parabola. During the lesson students will write quadratic functions when...
Texas Instruments
Texas Instruments: Transforming Parabolas
1. Students will be able to review how to find the vertex of a parabola using a graphing calculator. 2. Students will be able to observe the relationship between the values of a, h and k and the graph of a parabola in vertex form. 3....
Texas Instruments
Texas Instruments: Exploring the Parabola and Its Equation Part 1 and @
Starting with y=x^2 going all the way to (in part 2)y=ax^2+bx+c, how do changes in the quadratic equation/function change the appearance of the parabola.
Texas Instruments
Texas Instruments: Defining the Parabola
The teacher will graph a horizontal line and plot a point using TI-Navigator, and the class will provide the points that create a parabola.
Texas Instruments
Texas Instruments: Curve Fitting for a Parabola
This is a TI-Navigator Activity Center file that is used as a class warm up or for checking understanding. Students are to contribute an equation of a parabola that will pass through the most number of sunflowers.
Texas Instruments
Texas Instruments: Let's Play Ball With Families of Graphs
This activity is designed for students to use real-time data to generate a family of parabolic graphs. The data set will be generated by graphing the heights of a ball bounce with respect to time. Students will determine the regression...
Texas Instruments
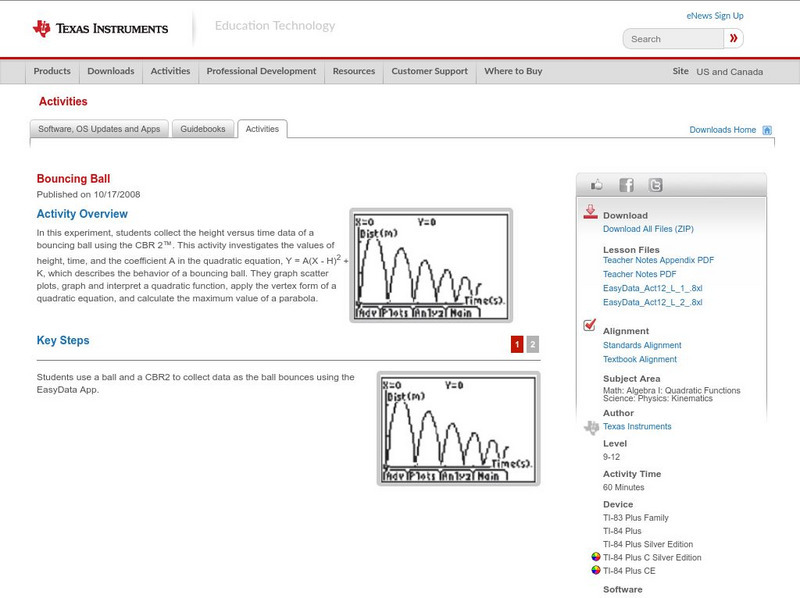
Texas Instruments: Bouncing Ball
In this experiment, students collect the height versus time data of a bouncing ball using the CBR 2. This activity investigates the values of height, time, and the coefficient A in the quadratic equation, which describes the behavior of...
University of Michigan
Virtual Conics
You may have to download first, but the two VRML icons near the bottom of the page allow you to observe the plane intersecting the cone to form the conic. Controls are present to change the angle of the plane and your view of the...
Science Education Resource Center at Carleton College
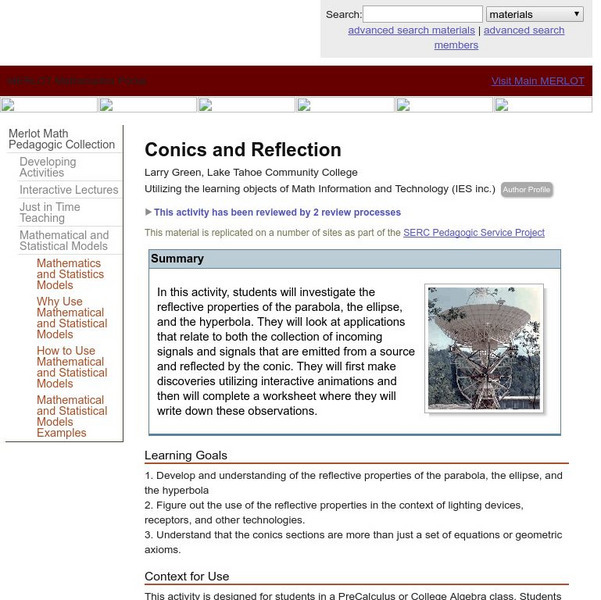
Serc: Conics and Reflection
Students investigate the reflective properties of the parabola, the ellipse, and the hyperbola. They will look at applications that relate to both the collection of incoming signals and signals that are emitted from a source and...
Stefan Warner and Steven R. Costenoble
Finite Mathematics & Applied Calculus: Quadratic Functions and Models
The resource investigates quadratic functions and models. Students learn about the concepts through notes and examples. A chapter quiz, review exercises, and chapter summary are included.
Ministry of Education and Universities of the Region of Murcia (Spain)
Ministerio De Educacion Y Ciencia: Conicas
In Spanish. Learn more about the ellipse, hyperbola and the parabola with these interactive activities.
Ministry of Education and Universities of the Region of Murcia (Spain)
Ministerio De Educacion Y Ciencia: Las Conicas
In Spanish. Learn how to distinguish and draw each of the conic sections with these activities.
Ministry of Education and Universities of the Region of Murcia (Spain)
Ministerio De Educacion Y Ciencia: Las Conicas
In Spanish. Learn about each of the conic sections with these interactive activities.