EngageNY
Translating Lines
Define parallel lines through transformations. The third lesson of 18 examines the result of the translation of a line. Two possible outcomes include coinciding lines and parallel lines.
EngageNY
Definition of Reflection and Basic Properties
Discover the results of reflecting an image. Learners use transparency paper to manipulate an image using a reflection in this fourth lesson of 18. They finish by reflecting various images across both vertical and horizontal lines.
EngageNY
Constant Rates Revisited
Find the faster rate. The resource tasks the class to compare proportional relationships represented in different ways. Pupils find the slope of the proportional relationships to determine the constant rates. They then analyze the...
EngageNY
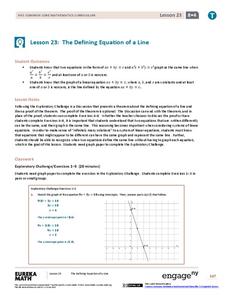
The Defining Equation of a Line
They appear to be different, yet they are the same line. Part 24 out of 33 lessons provides a theorem about the relationships of coefficients of equivalent linear equations. Pupils use the theorem to determine whether two equations are...
EngageNY
Cones and Spheres
Explore methods for finding the volume of different three-dimensional figures. The 20th lesson in the 25-part series asks learners to interpret diagrams of 3-D figures and use formulas to determine volume. Scholars must use the...
EngageNY
Ordering Integers and Other Rational Numbers
Scholars learn to order rational numbers in the seventh lesson in a series of 21. Reasoning about numbers on a number line allows for this ordering.
EngageNY
Distributions and Their Shapes
What can we find out about the data from the way it is shaped? Looking at displays that are familiar from previous grades, the class forms meaningful conjectures based upon the context of the data. The introductory lesson to...
EngageNY
Algebraic Expressions—The Distributive Property
Do your classes truly understand the distributive property? Use a demonstrative lesson plan to represent the distributive property in various ways. Learners solidify understanding by creating a geometric pattern for distributive...
EngageNY
Dividing the King’s Foot into 12 Equal Pieces
Apply, apply, apply! A measurement lesson applies a number of concepts to help learn a new construction. Scholars learn to divide a segment into n equal parts using a method that uses the Side Splitter Theorem and a method that...
EngageNY
Perimeter and Area of Polygonal Regions in the Cartesian Plane
How many sides does that polygon have? Building directly from activity number eight in this series, learners now find the area and perimeter of any polygon on the coordinate plane. They decompose the polygons into triangles and use...
EngageNY
Radicals and Conjugates
Make the irrational rational again! Continuing the theme from previous lessons in the series, the lesson plan relates the polynomial identity difference of squares to conjugates. Learners develop the idea of a conjugate through analysis...
EngageNY
Probability Rules (part 2)
Ensure your pupils are rule followers! Learners add the addition rule to the set of probability rules examined in the previous lesson. Problems require both the multiplication and addition rule.
EngageNY
Normal Distributions (part 2)
From z-scores to probability. Learners put together the concepts from the previous lessons to determine the probability of a given range of outcomes. They make predictions and interpret them in the context of the problem.
EngageNY
Margin of Error When Estimating a Population Proportion (part 2)
Error does not mean something went wrong! Learners complete a problem from beginning to end using concepts developed throughout the last five lessons. They begin with a set of data, determine a population proportion, analyze their result...
EngageNY
Ruling Out Chance (part 2)
Help your classes find the significance in this lesson! Learners analyze the probability of Diff values. They then determine if the difference is significant based on their probability of occurrence.
EngageNY
Rational Exponents—What are 2^1/2 and 2^1/3?
Are you rooting for your high schoolers to learn about rational exponents? In the third installment of a 35-part module, pupils first learn the meaning of 2^(1/n) by estimating values on the graph of y = 2^x and by using algebraic...
EngageNY
Four Interesting Transformations of Functions (Part 1)
Understanding how functions transform is a key concept in mathematics. This introductory lesson makes a strong connection between the function, table, and graph when exploring transformations. While the resource uses absolute value...
EngageNY
Four Interesting Transformations of Functions (Part 2)
What happens to a function whose graph is translated horizontally? Groups find out as they investigate the effects of addition and subtraction within a function. This nineteenth lesson in a 26-part series focuses on horizontal...
EngageNY
Four Interesting Transformations of Functions (Part 4)
What do you get when you cross piecewise functions with transformations? An engaging lesson! The conclusion of a four-part series on the transformations of functions asks class members to apply transformations to piecewise...
EngageNY
Graphing Quadratic Equations from the Vertex Form
Graphing doesn't need to be tedious! When pupils understand key features and transformations, graphing becomes efficient. This lesson connects transformations to the vertex form of a quadratic equation.
EngageNY
Recursive Formulas for Sequences
Provide Algebra I learners with a logical approach to making connections between the types of sequences and formulas with a lesson that uses what class members know about explicit formulas to develop an understanding of...
EngageNY
Base 10 and Scientific Notation
Use a resource on which you can base your lesson on base 10 and scientific notation. The second installment of a 35-part module presents scholars with a review of scientific notation. After getting comfortable with scientific...
EngageNY
An Appearance of Complex Numbers 2
Help the class visualize operations with complex numbers with a activity that formally introduces complex numbers and reviews the visualization of complex numbers on the complex plane. The fifth installment of a 32-part series...
EngageNY
The Geometric Effect of Some Complex Arithmetic 1
Translating complex numbers is as simple as adding 1, 2, 3. In the ninth lesson in a 32-part series, the class takes a deeper look at the geometric effect of adding and subtracting complex numbers. The resource leads pupils into what it...