CK-12 Foundation
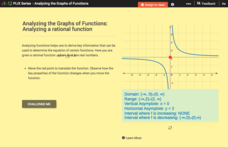
Analyzing the Graphs of Functions: Analyzing a Rational Function
Shift the function and transform the key features of the graph. By translating the graph of the rational function, class members find out how the key features alter. Pupils determine the domain, range, asymptotes, and intervals of...
CK-12 Foundation
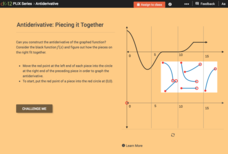
Antiderivative: Piecing it Together
Build a function backwards. Given a graph of the derivative of a function, pupils piece together a graph of the original function, the antiderivative. Learners use their graphs and the graphs of the derivatives to answer questions about...
CK-12 Foundation
Continuity at a Point, Continuity Test, Types of Discontinuity: Properties of Continuous Functions
Take a closer look at continuous functions within given intervals. Using the parent cubic function, learners explore properties of continuous functions on intervals. Pupils interpret the Intermediate Value Theorem and the Extreme Value...
CK-12 Foundation
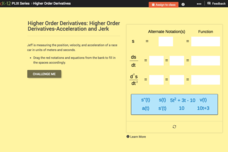
Higher Order Derivatives—Acceleration and Jerk
Accelerate your class through finding the second derivative. Using a bank of equations, pupils determine the equations for distance, velocity, and acceleration and their associated function notations. With the equations, learners answer...
CK-12 Foundation
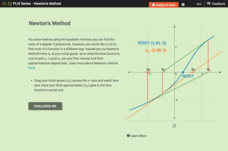
Newton's Method
Does the accuracy of the first guess make a difference down the line? Learners investigate the effects of the iterative process of finding roots, using Newton's Method. By moving the initial guess of a root on a graph, pupils observe the...
CK-12 Foundation
Tangent Line Approximation: Estimating Square Roots
Estimating a square root is as easy as evaluating a linear equation. Using the derivative of the square root function, pupils calculate an estimation of square roots. Class members determine the equation of the tangent line at the value...
CK-12 Foundation
Absolute Extrema and Optimization: Building the Biggest Box
Optimally, you want the largest box. Given a square piece of box material, pupils determine the size of congruent squares to cut out of the corners to create a box with the greatest volume. Learners determine the equation of the volume...
CK-12 Foundation
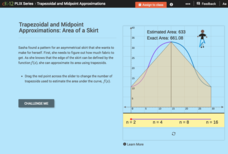
Trapezoidal and Midpoint Approximations: Area of a Skirt
When are trapezoids better than rectangles? Using trapezoids pupils approximate the area of fabric defined by a function. Just like with rectangles, learners realize the more trapezoids the more accurate the approximation. Scholars use...
CK-12 Foundation
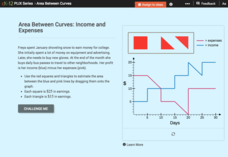
Area Between Curves: Income and Expenses
Use the area of polygons to calculate the area between curves. Pupils calculate areas under income and expense curves by filling the space with squares and right triangles. Using that information, they determine the profit related to the...
CK-12 Foundation
Method of Cylindrical Shells
Approximate the volume of a solid of revolution. Using a method similar to approximating the area under a curve, pupils investigate the volume of a solid of revolution. The learners use a given definite integral to find the volume of...
CK-12 Foundation
Differential Equations Representing Growth and Decay: Rice Legend
The legend of a wise man who asks a king for rice as a reward presents a context to study exponential solutions to differential equations. Pupils move quantities of rice to a chessboard and calculate the amount of rice for each day. To...
CK-12 Foundation
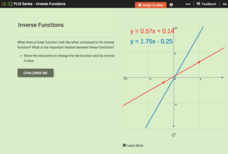
Inverse Functions
Provide a graphical view of inverses. Pupils manipulate points on a line and see the relationship of the graph with the graph of its inverse. Using the relationship between the graphs, scholars respond to questions concerning inverses...
CK-12 Foundation
Inverse Functions: Definition of Inverse Functions
Is the inverse of a function also a function? Pupils manipulate the graph of a function to view its inverse to answer this question. Using a horizontal and vertical line, class members determine whether the initial function is...
CK-12 Foundation
Explicit Formulas: Tiles for Writing nth Term in a Sequence
Build an explicit formula using tiles. Pupils develop a tile representation of a term within a sequence given figures of previous terms. Using the diagrams, learners develop the explicit formula by recognizing the common difference and...
CK-12 Foundation
Sum Notation and Properties of Sigma: Cracking the Code
Help your class develop an understanding of sigma notation. Pupils match the sigma notation with the sums. Using the expanded sums, learners evaluate the summations. The scholars move on to prove a property of sums.
CK-12 Foundation
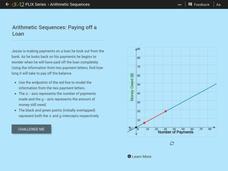
Arithmetic Sequences: Paying of a Loan
How long does it take to pay off a loan? Pupils use a graph to model the sequence associated with paying off a loan. Using the graph, learners determine the initial value and the common difference of the arithmetic sequence. The learners...
CK-12 Foundation
Finding the nth Term Given the Common Ratio and the First Term: Dominoes
Topple misunderstandings of geometric sequences. Using a context of creating ever-increasing sizes of dominoes, pupils develop a geometric sequence. The scenario provides the size of the first domino and the common ratio between...
CK-12 Foundation
Geometric Sequences: Bacteria Colony
Show budding mathematicians how to model a diminishing bacteria colony two ways—graphically and algebraically. Using the coordinate axis, pupils create a graph to represent the decay of a bacteria colony. They determine the number of...
CK-12 Foundation
Division of Decimals by Whole Numbers: Lemonade Stand
After a full day of selling lemonade, three friends split the cost of the profit money. If the total profit was $34.20, how much will each friend get?
CK-12 Foundation
Volume by Disks: The Vase Case
Finding the volume is an integral characteristic of a vase. Using the idea that summing the areas of cross-sectional disks will calculate the volume of a rotational solid, pupils find the volume of a vase. Scholars determine the interval...
CK-12 Foundation
Logarithm Properties: The Log Properties
Roll a log into an equivalent expression. Given four expanded logarithmic expressions, pupils write an equivalent condensed expression. They identify which properties allows for the simplification.
CK-12 Foundation
Sequence of Partial Sums: Partial Sums
Have some fun building squares out of triangles. Pupils investigate the partial sums of odd numbers. Using the sum of the first four odd numbers, learners see that it can be rewritten as a sum containing a triangular number. Simplifying...
CK-12 Foundation
Sums of Finite Arithmetic Series: Triangular Numbers
Using a slider, scholars build triangular numbers and their associated rectangles and use the geometric display to find the pattern to determine the next triangular number. They then relate that number to the area of the rectangle to...
CK-12 Foundation
Parabolas: Invisible Graph
Envision the function as the point swings. Given a point connected to another point and a line, pupils trace through an invisible graph. Learners identify the name of the given point and the line and determine the type of conic section...