CK-12 Foundation
Inverse Functions: Definition of Inverse Functions
Is the inverse of a function also a function? Pupils manipulate the graph of a function to view its inverse to answer this question. Using a horizontal and vertical line, class members determine whether the initial function is...
CK-12 Foundation
Vector Projection
Two words summarize the interactive: vector projector. An easy-to-use resource lets users investigate vector projections on the coordinate plane. Given the components of two vectors, they determine the projection of one vector onto the...
CK-12 Foundation
Vector Projection: Hitting a Baseball
Hit a home run with a resource that is all fun and games. Learners apply an interactive to determine the horizontal component of the distance a baseball travels. They must consider vector projections for this task.
CK-12 Foundation
Explicit Formulas: Tiles for Writing nth Term in a Sequence
Build an explicit formula using tiles. Pupils develop a tile representation of a term within a sequence given figures of previous terms. Using the diagrams, learners develop the explicit formula by recognizing the common difference and...
CK-12 Foundation
Sum Notation and Properties of Sigma: Cracking the Code
Help your class develop an understanding of sigma notation. Pupils match the sigma notation with the sums. Using the expanded sums, learners evaluate the summations. The scholars move on to prove a property of sums.
CK-12 Foundation
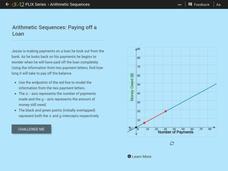
Arithmetic Sequences: Paying of a Loan
How long does it take to pay off a loan? Pupils use a graph to model the sequence associated with paying off a loan. Using the graph, learners determine the initial value and the common difference of the arithmetic sequence. The learners...
CK-12 Foundation
Finding the nth Term Given the Common Ratio and the First Term: Dominoes
Topple misunderstandings of geometric sequences. Using a context of creating ever-increasing sizes of dominoes, pupils develop a geometric sequence. The scenario provides the size of the first domino and the common ratio between...
CK-12 Foundation
Geometric Sequences: Bacteria Colony
Show budding mathematicians how to model a diminishing bacteria colony two ways—graphically and algebraically. Using the coordinate axis, pupils create a graph to represent the decay of a bacteria colony. They determine the number of...
CK-12 Foundation
Division of Decimals by Whole Numbers: Lemonade Stand
After a full day of selling lemonade, three friends split the cost of the profit money. If the total profit was $34.20, how much will each friend get?
CK-12 Foundation
Volume by Cross Section: Volume of the Cone
Discover another way to find the volume of a cone. Pupils explore how the area of a cross section changes as it moves through a cone. The interactive uses that knowledge to develop the integral to use to find the volume of the cone....
CK-12 Foundation
Volume by Disks: The Vase Case
Finding the volume is an integral characteristic of a vase. Using the idea that summing the areas of cross-sectional disks will calculate the volume of a rotational solid, pupils find the volume of a vase. Scholars determine the interval...
CK-12 Foundation
Logarithm Properties: The Log Properties
Roll a log into an equivalent expression. Given four expanded logarithmic expressions, pupils write an equivalent condensed expression. They identify which properties allows for the simplification.
CK-12 Foundation
Sequence: The Sequence Calculator
Work through a sequence in discovering number patterns. Using the interactive, pupils explore arithmetic and geometric sequences by setting the initial value and the common difference or ratio. Learners distinguish between the two types...
CK-12 Foundation
Arithmetic Series Sums: Adding Arithmetic Sums
Sum up the shortcuts. The interactive allows pupils to discover a shortcut in finding a partial sum of an arithmetic series. Learners use the shortcut to find other sums and to verify the process.
CK-12 Foundation
Sequence of Partial Sums: Partial Sums
Have some fun building squares out of triangles. Pupils investigate the partial sums of odd numbers. Using the sum of the first four odd numbers, learners see that it can be rewritten as a sum containing a triangular number. Simplifying...
CK-12 Foundation
Sums of Finite Arithmetic Series: Triangular Numbers
Using a slider, scholars build triangular numbers and their associated rectangles and use the geometric display to find the pattern to determine the next triangular number. They then relate that number to the area of the rectangle to...