K12 Reader
The Art of M.C. Escher
Show your class one way in which art and math are related by teaching them about M.C. Escher. Class members read a brief passage and then respond to five related questions.
National Gallery of Canada
Lumps, Bumps, Gritty, and Soft!
Texture can really add to a work of art. Explore texture through observation and practice. Learners view and discuss works of art by M.C. Escher. They then create their own texture samplers with six different materials.
Curated OER
Op Art Shapes
Op art is fun to look at, and it's fun to make. Kids learn about the origins of op art and the op art master, M.C. Escher. They view simple to complex examples of op art to see how it works and then create an optical piece of their own....
National Gallery of Canada
My Upside-Down World!
M.C. Escher is famous for creating optical illusions. Examine this effect in several of his works and discuss the techniques involved. Inspired by the discussion, learners create an imaginary 3-D world inside of a box using various...
National Gallery of Canada
Self-Portrait, Mirrors and Metamorphosis!
Using M.C. Escher's Hand with Reflecting Sphere as inspiration, learners create their own set of self-portraits using various reflective surfaces. The lesson begins with a discussion about portraiture and ends with a presentation of work...
Curated OER
Escher-Esque Tessellations
Middle and high schoolers participate in a seven-part lesson creating Escher-Esque tessellations. They demonstrate their knowledge of geometric transformations after viewing a PowerPoint presentation, conducting Internet research, and...
National Gallery of Canada
Tantalizing Tessellations!
Examine repeating and intricate patterns with a study of M.C. Escher and a related art activity. Pupils view and discuss the artwork before creating their own tessellating patterns. Step-by-step instructions for creating a template are...
Curated OER
The Wonderful World of Escher
Bridging art and math can be as easy as making tessellations. The art, context, and life of M.C. Escher is explained to the class, as is the concept of tessellations. After a bit of art history, pupils get out the ruler, tape, and...
Curated OER
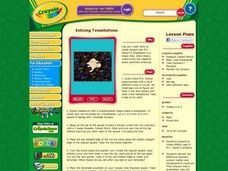
Enticing Tessellations
Learners respond to visual effects used in M.C. Escher's artworks. They identify the difference between subject matter and background of visual art. They compare and contrast the basic shapes to create a tessellation with the more...
Dick Blick Art Materials
Have a Ball!
M.C. Escher's "Hand with Reflecting Globe" and the work of Dick Termes, inspire this activity. Kids check out their reflection in a Christmas ornament or a bubble filter and recreate this distorted image on a vinyl ball.
Curated OER
Tantalizing Tessellations Lesson III: Creating a Slide Translation
Students explore tessellations and the artwork of M.C. Escher. They view and discuss a video about M.C. Escher, create a slide template out of cardboard, and create a poster with their tessellation pattern.
Curated OER
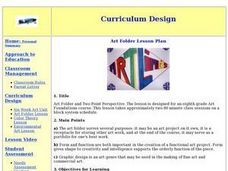
Art Folder and Two Point Perspective
Eighth graders examine how to create a 3-D effect on a flat surface and draw in two-point perspective. They view and discuss elements of design, analyze artwork by M.C. Escher and Roy Lichtenstein, and design and create an art folder.
Curated OER
Mathematics in Art?
Fifth graders view prints of M.C. Escher's work. They look at examples of geometric figures and polygons and discuss places they have seen them. Students create their own tessellations. They write a report about the process they used in...
Curated OER
What do two-dimensional tessellations look like? Where in art can they be found?
Students explore the world of art and culture, including the works of M.C. Escher. They identify and create original tessellations. Students use a wealth of interactive multimedia applications. They explore the artistic representations...
Curated OER
Mathematics and the Art of M.C. Escher
Students discover the connection between Escher's art and mathematics. They give various presentations based on their study.
Curated OER
Visual Arts: Matisse and Escher
Third graders are introduced to the art of Henri Matisse and M.C. Escher. They create original works in the styles of Matisse and Escher and consider how their innovations have affected modern art.
Curated OER
Three Arts in Retrograde
Students make connections between music, the other arts, and other curricular areas. They compare characteristics of two or more arts within a particular historical period or style and cite examples from various cultures.
Curated OER
M. C. Escher - Design - Math Integration
Students create a tessellations using rotation and translation. They also create a tessellation using reflection.
Curated OER
Tessellations and T-Shirts
Students combine the visual arts and technology with mathematics in the creation of these beautiful t-shirts. They view examples of the work of artist M.C. Escher.
Incredible Art
1, 2, and 3-Point Perspective
Introduce drawing students to perspective with a series of lesson that detail how to draft images in one-, two-, and three-point perspective. Each exercise includes step-by-step, illustrated directions and examples.
Curated OER
Terrific Tessellations
Learners create to pieces of artwork using two primary colors and tessellation techniques. This is an excellent lesson that can be accomplished using standard art techniques or educational software such as Adobe Photoshop or Microsoft...
Curated OER
Intuitive Approach to Limits
Students view examples of art work that illustrate limits in calculus. Students will lecture on limits and then complete practice drill. This lesson does not include a defined procedure or practice problems. All the art links work but...
Curated OER
Architecture
Students study tessellations and the work of M.C. Escher. They discuss the terminology of architecture, the historical significance of architecture in different parts of the world, and create their own piece of architecture out of...
Curated OER
Grade 5: Testing for Tessellations
Fifth graders use formal geometric language to describe polygons (and other shapes) that will tessellate the plane and those that will not. Students make generalizations about the characteristics of a polygon (or other shape) that will...