CK-12 Foundation
Pythagorean Theorem to Determine Distance: Neighborhood Map
Find the distance between various locations in a neighborhood. Scholars use the interactive to find distances between locations on a map. The map is overlaid onto a grid to provide coordinates for each location, and pupils apply...
CK-12 Foundation
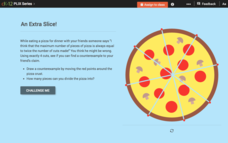
Conjectures and Counterexamples: An Extra Slice!
Class members will eat up an enticing interactive that lets users change the location of cuts made into a pizza to adjust the number of created slices. They create a counterexample for a conjecture on the number of slices.
Concord Consortium
Circling Trains
And round and round the park we go! Given a description of an amusement park with the locations of three attractions connected by walkways, learners consider what happens when additional attractions join the mix by doubling the length of...
Concord Consortium
Systematic Solution II
Up the difficulty level by solving a system of equations with variable coefficients. Young scholars devise a plan to solve for x and y in terms of a and b. They represent their solutions as expressions and explain their process and the...
Concord Consortium
School Bus Routes
Plan the way to school. Given a map of a school district, class members portray a transportation consultant hired to develop a bus transportation plan that will pick up the eligible riders and get them to school. The plan must contain...
Radford University
Throwing a Football
Use mathematics to help the football team. Pairs brainstorm how to approach finding a solution to a problem to help the quarterback complete more passes. By researching and collecting data, the teams derive an equation to represent the...
EngageNY
The Binomial Theorem
Sometimes, there is a better way. Scholars develop Pascal's triangle as a method to arrive at the coefficients of binomial expansions as an easier method to expand binomials. The learners connect the formula for binomial coefficients to...
EngageNY
The Binomial Theorem
Investigate patterns in the binomial theorem. Pupils begin by reviewing the coefficients from Pascal's triangle. They look at the individual terms, the sums of the coefficients on a row, and the alternating sum of each row. Individuals...
EngageNY
End Behavior of Rational Functions
Connect end behavior to previous learning. Pupils connect finding the end behavior of rational functions to finding end behavior of polynomial functions. The 13th segment in a 23-part unit starts with finding the end behavior or power...
EngageNY
Rational Functions
Make a connection between rational expressions and rational functions. Pupils review simplifying and performing operations on rational expressions and recall what it means for two rational expressions to be equivalent based on their...
EngageNY
Inverse Functions
Undo the functions. Learners refresh their knowledge of inverses of functions from Algebra II in the 19th section of a 23-part Precalculus unit. Pupils look at inverses in tables and graphs. They then add to their understanding of...
Curated OER
Get Ready, Get Set, PLAN
Students complete the theme activities in the unit for the month of September. In this planning lesson, students complete various themed activities for the month of September. Students complete movement activities, autonomy and social...
Curated OER
The Real Number System
Learners analyze the real number system. They discuss real numbers, rational and irrational numbers, integers, whole numbers, natural numbers and more of the real number in the system. They differentiate between all these numbers.
PBL Pathways
College Costs 2
What is the financial benefit for attending a community college for the first two years before transferring to a four-year college? The second part of the educational lesson asks young scholars to explore this question through data...
EngageNY
Graphs of Simple Nonlinear Functions
Time to move on to nonlinear functions. Scholars create input/output tables and use these to graph simple nonlinear functions. They calculate rates of change to distinguish between linear and nonlinear functions.
EngageNY
Sequencing Rotations
Discover the result of a sequence of rotations about different centers. Pupils perform rotations to examine the patterns. They also describe the sequence of rotations that performed to reach a desired result in the ninth installment in a...
EngageNY
Square Roots
Investigate the relationship between irrational roots and a number line with a resource that asks learners to put together a number line using radical intervals rather than integers. A great progression, they build on their understanding...
EngageNY
The Long Division Algorithm
Two methods are always better than one! The eighth installment in this series asks pupils to convert decimals to fractions using two approaches. Individuals first use the more traditional approach of long division and then use reverse...
EngageNY
Distance on the Coordinate Plane
Apply the Pythagorean Theorem to coordinate geometry. Learners find the distance between two points on a coordinate plane by using the Pythagorean Theorem. The vertical and horizontal change creates a right triangle, which allows...
EngageNY
Computing Actual Lengths from a Scale Drawing
The original drawing is eight units — how big is the scale drawing? Classmates determine the scale percent between a scale drawing and an object to calculate the length of a portion of the object. They use the percent equation to find...
EngageNY
The Relationship of Multiplication and Division
Take any number, multiply it by five, and then divide by five. Did you end up with the original number? In the same vein as the previous lesson, pupils discover the relationship between multiplication and division. They develop the...
EngageNY
Read Expressions in Which Letters Stand for Numbers III
Those key operation words sure come in handy. Groups continue their work with converting between different notations for algebraic expressions. They work in stations to write the symbolic form for given verbal phrases. This is the 17th...
EngageNY
Exponential Notation
Exponentially increase your pupils' understanding of exponents with an activity that asks them to explore the meaning of exponential notation. Scholars learn how to use exponential notation and understand its necessity. They use negative...
EngageNY
Introduction to Simultaneous Equations
Create an understanding of solving problems that require more than one equation. The lesson introduces the concept of systems of linear equations by using a familiar situation of constant rate problems. Pupils compare the graphs of...