Kenan Fellows
Half-Life
Scholars shake their way to understanding half-life with the help of candy. They observe and record which side candy lands on to graph the exponential decay in the fifth activity of seven integrating chemistry and algebra. Combining...
101 Questions
Fry's Bank
If money was left in an interest-earning account for 1,000 years, how much would it increase? Viewers watch a clip from a show about the future when someone learns about their balance after 1,000 years. Then, they solve for the amount in...
101 Questions
Double Sunglasses
If you wear two sets of sunglasses, do you get twice the darkness? Pupils explore an enlightening topic using a video and math model. They discover how to extend the topic through a sequel video and challenge question.
Howard County Schools
Drawing Inverses
An Algebra II lesson draws the connection between the exponential function and its inverse. By graphing an exponential function and using tables and a calculator, students graph the logarithmic function. The plan comes with a launch,...
Howard County Schools
Exponential Decay Exploration
How can you model exponential decay? Explore different situations involving exponential decay functions and decreasing linear functions by performing activities with MandM candy, popcorn kernels, and number cubes.
Howard County Schools
Getting Paid for School
What if you were paid to attend class? What kind of payment schedule would you choose? Learn how exponential functions will eventually exceed linear functions by comparing two different payment schedules for attending class.
Howard County Schools
Constant Rate Exploration
Question: What do rectangles and bathtub volume have in common? Answer: Linear equations. Learn how to identify situations that have constant rates by examining two different situations, one proportional and one not proportional.
Howard County Schools
Generous Aunt
Witness the power of exponential growth with an activity that investigates two different savings plans. Class members create tables of values to see how and when a savings plan increasing exponentially exceeds one increasing linearly.
Howard County Schools
Maria’s Quinceañera
How long will it take to save up for a car? Classmates use linear and exponential models to see how money received during a Quinceanera will grow over time.
Howard County Schools
Discounting Tickets
A boss who can't do math? Oh, no! Young entrepreneurs use linear and exponential models to determine which discount will yield the most profit on ticket sales.
101 Questions
Water Tank Filling
Grab your classes' attention with a video presentation of a problem to solve. Young scholars develop a plan to predict the time it takes to fill a tank with water. Video footage provides the statistics they need to make their conclusions.
101 Questions
Domino Skyscraper
Can a domino knock over a skyscraper? An inquiry-based lesson asks learners to calculate the size of domino needed to topple the Empire State Building. Using specific criteria and a geometric model, they find a solution.
101 Questions
The Incredible Shrinking Dollar
Make money disappear! Young scholars watch as a copier shrinks a dollar bill to 75 percent of its size. Learners are left to determine the size of the dollar bill after nine passes through the copier.
Alabama Learning Exchange
Logarithms: Undo the Exponential
Rumor has it that an exponential can be undone. After playing a rumor game to model exponential growth, pupils learn about undoing exponential functions. They use the definition of the logarithm to convert exponential equations to...
National Council of Teachers of Mathematics
National Debt and Wars
Take a functional approach to the national debt. Learners collect information about the national debt by decade and plot the data. They determine whether an exponential curve is a good fit for the data by comparing the percent changes...
Shodor Education Foundation
Function Flyer
Fly through graphing functions with the Function Flyer. Young mathematicians use an interactive to graph different types of functions. A set of exploration questions has users investigate patterns in functions.
Mathematics Assessment Project
Representing Functions of Everyday Situations
Functions help make the world make more sense. Individuals model real-world situations with functions. They match a variety of contexts to different function types to finish a helpful resource.
CK-12 Foundation
Geometric Sequences: Bacteria Colony
Show budding mathematicians how to model a diminishing bacteria colony two ways—graphically and algebraically. Using the coordinate axis, pupils create a graph to represent the decay of a bacteria colony. They determine the number of...
CK-12 Foundation
Sequence: The Sequence Calculator
Work through a sequence in discovering number patterns. Using the interactive, pupils explore arithmetic and geometric sequences by setting the initial value and the common difference or ratio. Learners distinguish between the two types...
CPALMS
Writing an Exponential Function from its Graph
Grow an equation for the exponential graph. Given a graph of an exponential function, class members write the equation of the function provided. The graph labels two points on the graph: the y-intercept and the point where x is one.
Mathematics Vision Project
Connecting Algebra and Geometry
Connect algebra and geometry on the coordinate plane. The eighth unit in a nine-part integrated course has pupils develop the distance formula from the Pythagorean Theorem. Scholars prove geometric theorems using coordinates including...
Mathematics Vision Project
Features of Functions
What are some basic features of functions? By looking at functions in graphs, tables, and equations, pupils compare them and find similarities and differences in general features. They use attributes such as intervals of...
Mathematics Vision Project
Linear and Exponential Functions
Provide a continuous progression to linear and exponential functions. Pupils continue to work with the discrete functions known as sequences to the broader linear and exponential functions. The second unit in a series of nine provides...
CK-12 Foundation
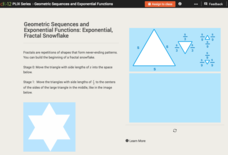
Exponential Growth: Exponential, Fractal Snowflakes
Examine an exponential growth model. Using a fractal, learners calculate the perimeters of each stage. When comparing the consecutive perimeters, a pattern emerges. They use the pattern to build an equation and make conclusions.