Illustrative Mathematics
Illustrative Mathematics: G Mg Hexagonal Pattern of Beehives
Beehives are made of walls, each of the same size, enclosing small hexagonal cells where honey and pollen are stored and bees are raised. This problem examines some of the mathematical advantages of the hexagonal tiling in a beehive....
Illustrative Mathematics
Illustrative Mathematics: G Mg Toilet Roll
Picture a roll of toilet paper; assume that the paper in the roll is very tightly rolled. Assuming that the paper in the roll is very thin, find a relationship between the thickness of the paper, the inner and outer radii of the roll,...
Illustrative Mathematics
Illustrative Mathematics: G Mg How Many Cells Are in the Human Body?
About how many cells are in the human body? The purpose of this task is for students to apply the concepts of mass, volume, and density in a real-world context. Aligns with G-MG.A.2.
Illustrative Mathematics
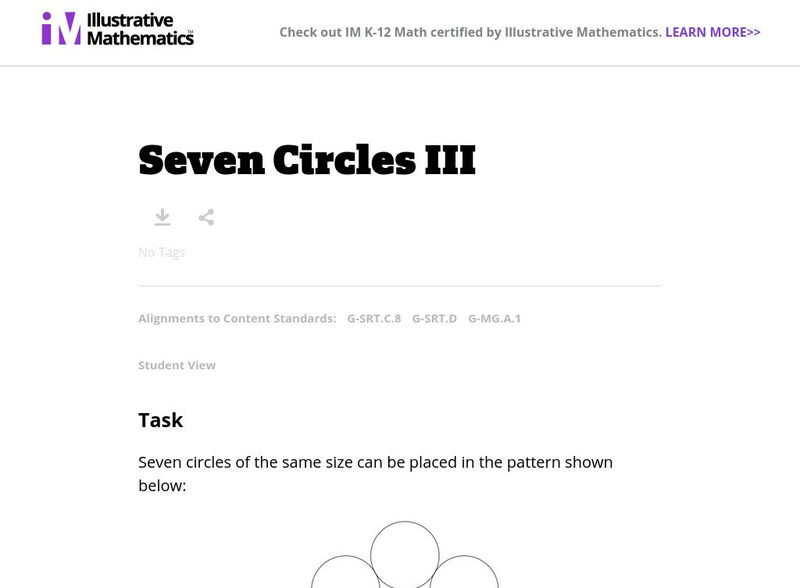
Illustrative Mathematics: G Srt, G Mg Seven Circles Iii
In this task, students are shown circle formations where an inner circle is surrounded by a set of circles and all circles are touching. In the first situation, all circles have the same diameter. In the second, the inner circle is...
Illustrative Mathematics
Illustrative Mathematics: G Srt, G Mg How Far Is the Horizon?
Some friends are at the beach looking out onto the ocean on a clear day and they wonder how far away the horizon is. A second problem asks how far the horizon would be from the top of a mountain. Students must also answer a question...
Illustrative Mathematics
Illustrative Mathematics: G Gmd, G Mg Tennis Balls in a Can
In this task, students investigate the volume of tennis balls and their cylindrical container, the empty space around the balls, different ways of slicing them, and what their visualizations will look like. Aligns with G-GMD.B.4 and...
Illustrative Mathematics
Illustrative Mathematics: G Mg the Lighthouse Problem
For this task, students are asked to calculate the height above sea level of a lamp on top of a lighthouse that is visible to a boat, and to examine two other interpretations of the distance from the lighthouse to the boat. Aligns with...
Illustrative Mathematics
Illustrative Mathematics: G Mg, G Gmd Global Positioning System Ii
Satellites communicate with a GPS device and establish the distance between them and their locations. The set of points at a fixed distance from a satellite form a sphere so when the GPS receives its distance from a given satellite, this...
Illustrative Mathematics
Illustrative Mathematics: G Mg How Thick Is a Soda Can? Variation Ii
In this task, learners are given an aluminum soda can and are simply asked how they could determine how thick the can is. Aligns with G-MG.A.1 and G-MG.A.2.
Illustrative Mathematics
Illustrative Mathematics: G Mg How Thick Is a Soda Can? Variation I
For this task, students are given the dimensions of a soda can and are asked to estimate its thickness. They must first find the surface area and the volume of aluminum. Aligns with G-MG.A.1 and G-MG.A.2.
Illustrative Mathematics
Illustrative Mathematics: G Mg Solar Eclipse
In this task, students investigate why total solar eclipses are rare. They will learn that, in addition to requiring the positioning of the Sun, Moon, and Earth, the Moon can only completely block out the Sun when it is closest to the...
Illustrative Mathematics
Illustrative Mathematics: G Mg Tilt of Earth's Axis and the Four Seasons
This task gives students a chance to explore the effects of the Earth's tilt and rotation using a simple geometric model of Earth-Sun interaction that shows why the seasons occur. Aligns with G-MG.A.1.
Illustrative Mathematics
Illustrative Mathematics: G Mg How Many Leaves on a Tree? (Version 2)
For this task, students must estimate the number of leaves on a large tree, taking into account various complex factors such as the area shaded by the tree, the area of irregularly shaped leaves, the uneven distribution of leaves, the...
Illustrative Mathematics
Illustrative Mathematics: G Mg How Many Leaves on a Tree?
This is a mathematical modeling task aimed at making a reasonable estimate for something which is too large to count accurately, the number of leaves on a tree, taking into account the tree size and the density of the leaves. Aligns with...