Illustrative Mathematics
Right Triangles Inscribed in Circles I
One of the basic properties of inscribed angles gets a triangle proof treatment in a short but detailed exercise. Leading directions take the learner through identifying characteristics of a circle and how they relate to angles and...
Illustrative Mathematics
Right Triangles Inscribed in Circles II
So many times the characteristics of triangles are presented as a vocabulary-type of instructional activity, but in this activity they are key to unraveling a proof. A unique attack on proving that an inscribed angle that subtends a...
Mathematics Vision Project
Congruence, Construction and Proof
Learn about constructing figures, proofs, and transformations. The seventh unit in a course of nine makes the connections between geometric constructions, congruence, and proofs. Scholars learn to construct special quadrilaterals,...
Inside Mathematics
Circles in Triangles
Challenge the class with inscribed circles in triangles. The assessment task requests class members use their knowledge of circles and right triangles to prove two triangles are congruent. They go on to utilize their knowledge of...
Mathematics Vision Project
Module 2: Congruence, Construction and Proof
Construct yourself a winning geometry unit. A set of lessons introduces geometry scholars to constructions and proofs with compasses and straightedges. It also covers triangle congruence through transformations. This is the second of...
Illustrative Mathematics
Tangent to a Circle From a Point
Learners see application of construction techniques in a short but sophisticated problem. Combining the properties of inscribed triangles with tangent lines and radii makes a nice bridge between units, a way of using...
EngageNY
Unknown Angle Problems with Inscribed Angles in Circles
We know theorems about circles—now what? Class members prove a theorem, with half the class taking the case where a point is inside the circle and half the class taking the case where a point is outside the circle. The lesson then...
EngageNY
Ptolemy's Theorem
Everyone's heard of Pythagoras, but who's Ptolemy? Learners test Ptolemy's Theorem using a specific cyclic quadrilateral and a ruler in the 22nd installment of a 23-part module. They then work through a proof of the theorem.
Curated OER
Inscribed Angles
In this inscribed angles worksheet, 10th graders solve 13 various types of problems related to inscribed angles in geometry. First, they identify a circle illustrated and each arc of the circle. They, students find the measure of each...
Illustrative Mathematics
Applying the Pythagorean Theorem in a Mathematical Context
Participants who use this resource will apply the Pythagorean Theorem to show whether or not the shaded triangle inscribed in a rectangle is a right triangle. Once all of the sides on the shaded triangle are found, it is important that...
Mathematics Vision Project
Module 6: Congruence, Construction, and Proof
Trace the links between a variety of math concepts in this far-reaching unit. Ideas that seem very different on the outset (like the distance formula and rigid transformations) come together in very natural and logical ways. This...
EngageNY
Thales’ Theorem
Isn't paper pushing supposed to be boring? Learners attempt a paper-pushing puzzle to develop ideas about angles inscribed on a diameter of a circle. Learners then formalize Thales' theorem and use geometric properties to develop a proof...
Mathematics Vision Project
Circles: A Geometric Perspective
Circles are the foundation of many geometric concepts and extensions - a point that is thoroughly driven home in this extensive unit. Fundamental properties of circles are investigated (including sector area, angle measure, and...
Virginia Department of Education
High School Mathematics Geometry Vocabulary Word Wall Cards
Having a good working knowledge of math vocabulary is especially important for geometry learners. Here are 119 pages worth of wonderfully constructed definitions, constructions, formulas, properties, theorems, and postulates. This is a...
EngageNY
Tangent Segments
What's so special about tangents? Learners first explore how if a circle is tangent to both rays of an angle, then its center is on the angle bisector. They then complete a set of exercises designed to explore further properties and...
Maths Challenge
Maths challenge.net: Triangle in a Square
A "three star" geometry problem requiring some prior knowledge in math and proofs to maximize the area of an inscribed triangle in terms of the hypotenuse.
CK-12 Foundation
Ck 12: Geometry: Inscribed Similar Triangles
[Free Registration/Login may be required to access all resource tools.] Apply the fact that the altitude of a right triangle creates similar triangles.
Science Buddies
Science Buddies: Inscribing a Circle in a Triangle Using the Geometry Applet
Here is a project that combines Computer Science and Mathematics. Prove a method for inscribing a circle within a triangle (as shown). You'll also learn how to create an interactive diagram to illustrate your proof, using an applet that...
Cut the Knot
Cut the Knot: Existence of the Orthocenter
This site defines the altitude of a triangle and gives the standard notation for altitudes of a triangle. The site then goes to list several proofs involving altitudes and orthocenters.
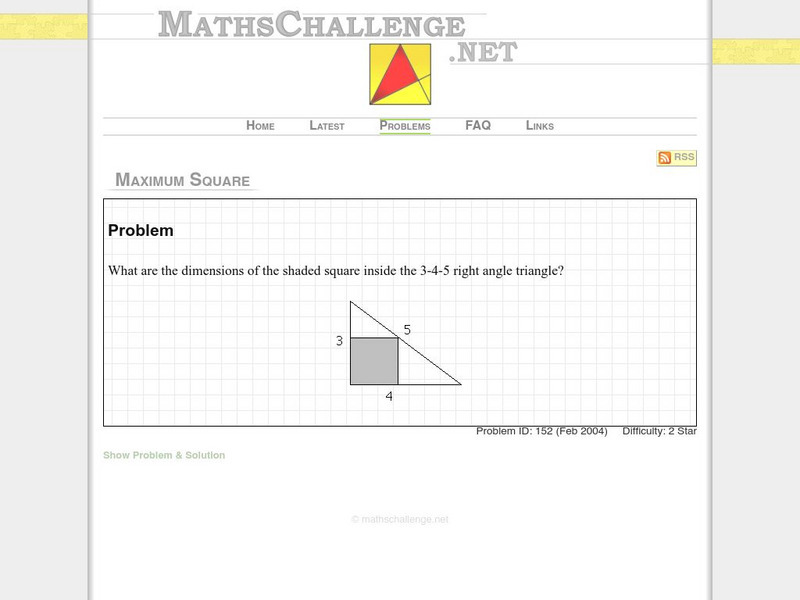
Maths Challenge
Maths challenge.net: Maximum Square
A challenging proof like geometry of finding the square inscribed in a triangle.
Illustrative Mathematics
Illustrative Mathematics: G C Locating Warehouse
You have been asked to place a warehouse so that it is an equal distance from three roads on a map. Students must fold a paper so that this point is where two folds intersect, and they must explain why their construction works and why...
Illustrative Mathematics
Illustrative Mathematics: G C Placing a Fire Hydrant
You have been asked to place a fire hydrant so that it is an equal distance from three locations on a map. Students must fold a paper so that this point is where two folds intersect, and they must explain why their construction works and...